
БРАУЭРА-СЕВЕРИ МНОГООБРАЗИЕ
Расстановка ударений: БРА`УЭРА-СЕ`ВЕРИ МНОГООБРА`ЗИЕ
БРАУЭРА-СЕВЕРИ МНОГООБРАЗИЕ - алгебраическое многообразие над полем k, которое, если его рассматривать над алгебраич. замыканием k¯ поля k, изоморфно проективному пространству.
Арифметич. свойства таких многообразий изучал Ф. Севери (F. Severi, 1932), позднее Ф. Шатле [1] вскрыл связь Б.-С. м. с центральными простыми алгебрами над полем k и с Брауэра группой.
Простейшим нетривиальным примером одномерного Б.-С. м. является проективная коника Q:
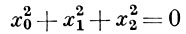
на действительной проективной плоскости Р2ℝ . Над полем комплексных чисел ℂ это многообразие изоморфно проективной прямой Р1ℝ . Множество всех одномерных Б.-С. м. (рассматриваемых с точностью до изоморфизма) находится во взаимно однозначном соответствии с множеством проективных невырожденных коник (рассматриваемых с точностью до проективной эквивалентности над k), к-рое, в свою очередь, находится во взаимно однозначном соответствии с множеством (неизоморфных) алгебр обобщенных кватернионов над k. В приведенном выше примере конике Q соответствует алгебра обычных кватернионов.
В многомерном случае множество классов n-мерных Б.-С. м. (т. е. множество Б.-С. м., различаемых с точностью до k-изоморфизма) может быть отождествлено с множеством Галуа когомологий H1 (k, PGL(n + 1, k)), где PGL(n + 1, k)-проективная группа автоморфизмов проективного пространства Рnk (см. [3], [4]). Этим же множеством когомологий описываются классы k-изоморфных центральных простых k-алгебр ранга (n + 1)2 (т. е. форм матричной алгебры Мn + 1 (k)). Более явно связь Б.-С. м. с центральными простыми алгебрами устанавливается следующим образом, k-алгебре А ранга r2 сопоставляется многообразие X ее левых идеалов ранга r, к-рое задается как замкнутое подмногообразие в Грассмана многообразии всех k-линейных подпространств размерности r в А. В нек-рых случаях многообразие А можно задать с помощью норменных уравнений, как, например, в случае алгебр кватернионов. Взаимосвязь Б.-С. м. и алгебр существенно используется при изучении как тех, так и других (см. [1], [4]).
Наиболее существенными свойствами Б.-С. м. являются следующие. Б.-С. м. X тогда и только тогда k-изоморфно проективному пространству Рnk, когда оно имеет точку в поле k. Любое Б.-С. м. имеет точку в нек-ром конечном сепарабельном расширении К поля k (см. [1]).
Для Б.-С. м., определенных над полем алгебраич. чисел, справедлив Хассе принцип.
Поле рациональных функций k(X) на Б.-С. м. X является полем разложения соответствующей алгебры А; более того, произвольное расширение К поля k тогда и только тогда является полем разложения для А, когда X имеет K-точку (см. [4]).
В связи с обобщением на схемы понятий центральной простой алгебры и группы Брауэра было введено понятие схем Брауэра-Севери, обобщающее понятие Б.-С. м. (см. [2]). Пусть f : Р → X - морфизм схем. Схема Р наз. схемой Брауэра-Севери, если локально, в этальной топологии схемы X, схема Р изоморфна проективному пространству РnX над X. Схема Р над схемой X тогда и только тогда является схемой Брауэра-Севери, когда f : Р → X - конечно представленный собственный плоский морфизм и все геометрич. слои его изоморфны проективным пространствам [2].
Лит. : [1] Châtelet F., «Аnn. École Normal supereur», 1944, t. 61, p. 249-300; [2] Grоthendieсk A., Le groupe de Brauer, в кн. : Seminaire Bourbaki, аnnéе 17, 1964/65, N. Y. - Amst., exposes 290, p. 1-21; [3] Gepp Ж.-П., Когомологии Галуа, пер. с франц., М., 1968; [4] Рокетт П., «Математика», 1967, т. 11, в. 5, с. 88-116.
В. А. Исковских.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'