БРАУЭРА ГРУППА

Расстановка ударений: БРА`УЭРА ГРУ`ППА

БРАУЭРА ГРУППА поля k - группа классов конечномерных центральных простых алгебр над полем k, относительно эквивалентности, определенной следующим образом. Две центральные простые k-алгебры А и В конечного ранга эквивалентны, если существуют такие целые положительные числа тип, что тензорные произведения A⊗_k M_m (k) и В⊗_k М_n (k) являются изоморфными k-алгебрами (здесь М_r (k) алгебра квадратных матриц порядка r над k). Тензорное умножение алгебр индуцирует на множестве классов эквивалентных центральных простых конечномерных алгебр структуру абелевой группы, к-рая и наз. Б. г. поля k и обозначается ВrK;. Нулевым элементом этой группы служит класс полных матричных алгебр, а обратным элементом к классу алгебры А - класс ее инверсной алгебры. Каждый ненулевой класс содержит ровно одну, с точностью до изоморфизма, k-алгебру с делением (т. е. тело над k).

Б. г. была определена и изучалась в серии работ Р. Брауэра (В. Brauer), Э. Нётер (Е. Noether), А. Алберта (A. Albert), X. Хассе (Н. Hasse) и др. начиная с 20-х гг. 20 в. (см., напр., [6]). Наиболее законченные результаты, вплоть до полного вычисления Б. г., были получены для числовых полей в связи с развитием полей классов теории. В терминах Б. г. формулируется общая форма закона взаимности.

Б. г. равна 0 для любого сепарабельно замкнутого поля и любого конечного поля. Для поля действительных чисел Б. г. есть циклич. группа 2-го порядка и ее ненулевой элемент - класс алгебры кватернионов. Если k - поле р-адических чисел или любое полное дискретно нормированное локально компактное поле, то его Б. г. изоморфна Q/Z (здесь Q - аддитивная группа рациональных чисел, Z - аддитивная группа целых чисел). Этот факт занимает важное место в локальной теории полей классов.

Пусть k - поле алгебраич. чисел конечной степени или поле алгебраич. функций от одной переменной с конечным полем констант. Тогда имеет место точная последовательность групп:

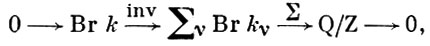
где ν пробегает всевозможные нормирования поля k, k, - соответствующие пополнения поля k, гомоморфизм inv индуцируется естественными вложениями k → k_ν . Образ элемента из Вг k в Br k_ν наз. локальным инвариантом, гомоморфизм Σ является суммированием локальных инвариантов. Этот факт устанавливается в глобальной теории полей классов. Если k - поле алгебраич. функций от одной переменной над алгебраически замкнутым полем констант, то его Б. г. нулевая (теорема Тзена). Случай произвольного поля констант разобран в [4] и [7].

Б. г. функториально зависит от k, т. е. если K - расширение поля k, то определен гомоморфизм Вr k → Вr K. Его ядро, обозначаемое Вr(К/k), состоит из классов алгебр, распадающихся над K.

Конструкции скрещенных произведений с помощью систем факторов (см. [5]) приводят к когомологич. интерпретации Б. г. Для любого нормального расширения К/k имеет место изоморфизм

Вr (К/k) ≅ H² (K, K*),

где H² (K', K*) - группа двумерных когомологий Галуа с коэффициентами в мультипликативной группе K* поля K. Более того, группа Вrk изоморфна H² (k¯, k¯ *), где k¯ - сепарабельное замыкание поля k. Сопоставление центральной простой алгебре ее класса в Б. г. осуществляется при помощи кограничного оператора

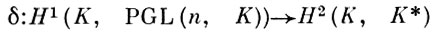
в когомологич. последовательности, соответствующей точной последовательности групп

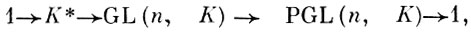
где GL(n, K) и PGL(n, К) - линейная и проективная группы матриц порядка n × n. Здесь группа H¹ (K, PGL(n, K)) интерпретируется как множество классов с точностью до k-изоморфизма центральных простых алгебр ранга n² над полем k, распадающихся над k, или как множество классов k-изоморфных Брауэра-Севери многообразий размерности n - 1, имеющих X-точку.

Б. г. всегда является периодической группой. Порядок любого ее элемента делит число n, где n² - ранг тела, представляющего этот элемент.

Когомологич. интерпретация Б. г. позволяет рассматривать ее как группу классов центральных расширений группы Галуа сепарабельного замыкания k¯ /k при помощи группы k¯ *.

Обобщением понятия Б. г. является группа Брауэра-Гротендика, определяемая аналогично Б. г. с заменой центральных простых алгебр на алгебры Адзумая (см. [7]).

Лит. : [1] Алгебраическая теория чисел, пер. с англ., М., 1969; [2] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [3] Серр Ж.-П., Когомологий Галуа, пер. с франц., М., 1968; [4] Фаддеев Д. К., «Вестник Ленингр. ун-та», 1957, № 7, в. 2, с. 45-51; [5] Чеботарев Н. Г., Введение в теорию алгебр, М. - Л., 1949; [6] Dеuring М., «Algebren», 2 Aufl., В., 1968, Bd 4; [7] Grоthеndieсk A., в кн. : Dix exposes sur la cohomologie des schemax, Amst., 1968, p. 46-188.

В. А. Исковских.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.