БОХНЕРА-МАРТИНЕЛЛИ ПРЕДСТАВЛЕНИЕ

Расстановка ударений: БО`ХНЕРА-МАРТИНЕ`ЛЛИ ПРЕДСТАВЛЕ`НИЕ

БОХНЕРА-МАРТИНЕЛЛИ ПРЕДСТАВЛЕНИЕ, Мартинелли-Бохнера представление, Мартинелли-Бохнера формула, - интегральное представление голоморфных функций, определяемое следующим образом (см. [1], [2]). Пусть функция f голоморфна в области D ⊂ ℂⁿ с кусочно гладкой границей ∂D и непрерывна в ее замыкании D¯. Тогда выражение

(*)

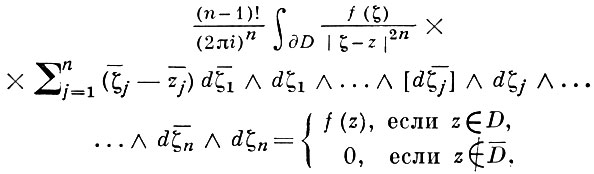
где [dζ¯_j ] означает, что член dζ¯_j следует опустить, наз. Б.-М. п. При n = 1 Б.-М. п. совпадает с интегральной формулой Коши (см. Коши интеграл), однако при n > 1 его ядро не является голоморфным по z, и этим объясняется ограниченность применения Б.-М. п. в теории функций многих комплексных переменных. Ядром Б.-М. п. является дифференциальная форма по ζ бистепени (n, n - 1):

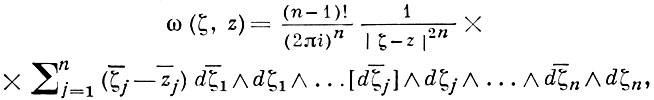
определенная в ℂⁿ, с особенностью в точке ζ = z, ∂¯ - замкнутая (т. е. ∂¯ ω = 0) вне особенности. При n > 1 форма со равна ∂ω '(ζ', z), где

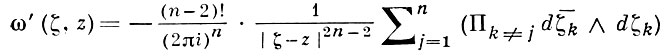
- форма бистепени (n - 1, n - 1), коэффициент к-рой является фундаментальным решением уравнения Лапласа; здесь

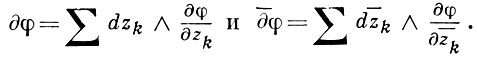
Следующее интегральное представление, обобщающее формулу (*), является аналогом формулы Коши-Грина (см. Коши интеграл): если функция f непрерывно дифференцируема в замыкании области D ⊂ ℂⁿ с кусочно гладкой границей ∂D, то для всякой точки z ∈ D

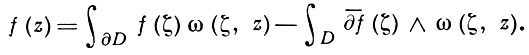
Функция

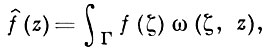
где Г - гладкая гиперповерхность в ℝ²ⁿ = ℂⁿ и f - функция на Г, интегрируемая по мере Лебега, наз. интегралом типа Бохнера-Мартинелли. Как и для интегралов типа Коши, для интегралов типа Бохнера-Мартинелли справедлива формула Сохоцкого при обычных ограничениях на Г и f. Интеграл типа Бохнера-Мартинелли является комплексной функцией, гармонической всюду вне Г; в общем случае эта функция голоморфна лишь при n = 1. Если T = ∂D, то при n ≥ 1 условие f^(z) ≡ 0 вне D¯ эквивалентно голоморфности f в D.

Б.-М. п. используется для вывода других интегральных представлений (напр., Бергмана-Вейля представления), для голоморфного продолжения с границы, а также в теории граничных значений голоморфных функций нескольких комплексных переменных. Б.-М. п. получено С. Бохнером и Э. Мартинелли (см. [1], [2]).

Лит. : [1] Восhnеr S., «Аnn. Math. », 1943, v. 44, №4, p. 652-673; [2] Martinelli E., «Rend. Accad. Italia», 1938, v. 9, p. 269-83; [3] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964.

Е. М. Чирка.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.