БОХНЕРА ИНТЕГРАЛ

Расстановка ударений: БО`ХНЕРА ИНТЕГРА`Л

БОХНЕРА ИНТЕГРАЛ - интеграл от функции со значениями в банаховом пространстве по скалярной мере. Б. и. принадлежит к так наз. сильным интегралам.

Пусть F (X; Е, 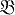, μ) - векторное пространство функций х(t), t ∈ Е, со значениями и банаховом пространстве X, заданных на пространстве (Е, 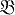, μ) со счетно аддитивной скалярной мерой μ на σ - алгебре 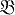подмножеств множества Е. Функция x₀ (t) ∈ F наз. простой, если

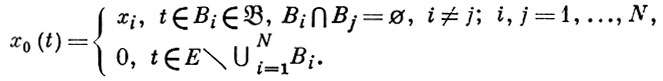
Функция x(t) ∈ F наз. сильно измеримой, если существует последовательность {x_n (t)} простых функций и ||x(t) - x_n (t)|| → 0 почти всюду относительно меры μ на Е. В этом случае скалярная функция ||x(t)|| является - измеримой. Для простой функции x₀ (t)

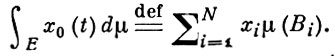
Функция x(t) наз. интегрируемой по Бохнеру, если она сильно измерима и если для любой аппроксимирующей последовательности {x_n (t)} простых функций

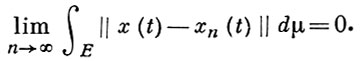
Для такой функции интегралом Бохнера по множеству В ∈ наз.

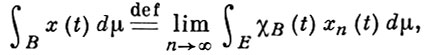
где χ_B (f) - характеристич. функция множества В, а предел понимается в смысле сильной сходимости в банаховом пространстве X. Этот предел существует и не зависит от выбора аппроксимирующей последовательности простых функций.

Критерий интегрируемости по Б о х н е р у: для того чтобы сильно измеримая функция x(t) ∈ F была интегрируема по Бохнеру, необходимо и достаточно, чтобы норма этой функции была интегрируема, т. е.

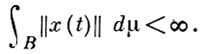
Множество функций, интегрируемых по Бохнеру, образует векторное подпространство ℒ пространства F, а Б. и. есть аддитивный и однородный оператор на этом подпространстве.

Свойства Б. и. :

1)

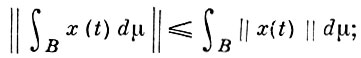
2) Б. и. есть счетно аддитивная и абсолютно непрерывная функция множеств σ - алгебры 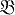, т. е.

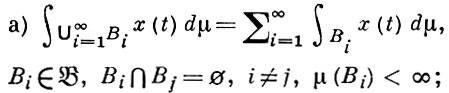
б) 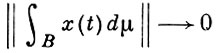при μ (B) → 0 равномерно по В ∈ ;

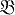3) если x_n (t) ∈ F, x_n (t) = X(t) почти всюду относительно меры μ на В ∈ 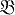и ||х_n (t)|| ≤ f(t) почти всюду относительно μ на В, причем

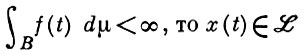
и

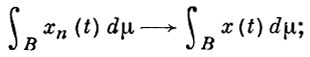
4) пространство ℒ полно относительно сходимости по норме

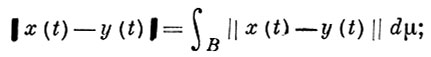
5) если T - замкнутый линейный оператор из банахова пространства х в банахово пространство у и

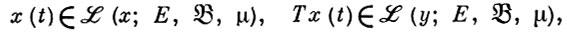
то

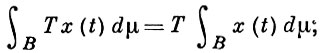
в случае ограниченности Т условие

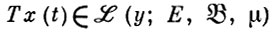
выполняется автоматически ([3]-[5]).

Б. и. введен С. Бохнером [1]. Эквивалентные определения даны Т. Гильденбрандтом [2] и Н. Данфордом (интеграл D₀).

Лит. : [1] Воchner S., «Fundam. math. », 1933, t. 20, p. 262-76; [2] Hildebrandt Т., «Bull. Amer. Math. Soc. », 1953, v. 59; p. 111-39; [3] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [4] Xилле Э., Филлипс Р., Функциональный анализ и полугруппы, пер. с англ., [2 изд.], М., 1962; [5] Данфорд Н., Шварц Дж. Т., Линейные операторы, пер. с англ., т. 1 - Общая теория, М., 1962.

В. И. Соболев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.