БОРЕЛЯ-ЛЕБЕГА ТЕОРЕМА

Расстановка ударений: БОРЕ`ЛЯ-ЛЕ`БЕГА ТЕОРЕ`МА

БОРЕЛЯ-ЛЕБЕГА ТЕОРЕМА о покрытии: пусть А - ограниченное замкнутое множество в Rⁿ и G его открытое покрытие, т. е. система открытых множеств, объединение к-рых включает А; тогда существует конечная подсистема множеств {G_i} n = 1, 2, ..., N, из G (подпокрытие), также являющаяся покрытием А, т. е.

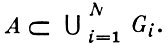
Б.-Л. т. обратима: если A ⊂ Rⁿ и из любого открытого покрытия А можно выделить конечное подпокрытие, то А замкнуто и ограничено. Возможность выделения конечного подпокрытия из любого открытого покрытия множества А часто принимается за определение множества А как компакта. В такой терминологии Б.-Л. т. вместе с обратной принимает вид: чтобы множество A ⊂ Rⁿ было компактом, необходимо и достаточно, чтобы А было ограниченным и замкнутым. Б.-Л. т. была в 1898 доказана Э. Борелем (см. [1]) в случае, когда А есть отрезок [a, b] ⊂ R¹ и G есть система интервалов, окончательную форму получила в 1900-10 в работах А. Лебега (см. [2]). Б.-Л. т. называют иногда также леммой Бореля, леммой Гейне-Бореля, теоремой Гейне-Бореля.

Лит. : [1] Вorel Е., Lecons sur la theorie des fonctions, 3 ed., P., 1928; [2] Рудин У., Основы математического анализа, пер. с англ., М., 1966.

И. А. Виноградова.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.