БОРЕЛЯ ПОДГРУППА

Расстановка ударений: БОРЕ`ЛЯ ПОДГРУ`ППА

БОРЕЛЯ ПОДГРУППА, борелевская подгруппа, - максимальная связная разрешимая алгебраич. подгруппа линейной алгебраической группы G. Напр., подгруппа всех невырожденных верхних треугольных матриц является Б. п. в полной линейной группе GL(n). Систематич. исследование максимальных связных разрешимых подгрупп алгебраич. групп впервые проведено А. Борелем [1]. Б. п. может быть эквивалентным образом определена как минимальный элемент множества параболических подгрупп, т. е. таких алгебраич. подгрупп Н группы G, для к-рых фактормногообразие G/H проективно. Все Б. п. группы G сопряжены, причем, если Б. п. B₁, B₂ и группа G определены над полем k, то В₁ и B₂ сопряжены посредством элемента из G_k . Пересечение любых двух Б. п. группы G содержит максимальный тор группы G; если это пересечение есть в точности максимальный тор, то такие Б. п. наз. противоположными. Противоположные Б. п. существуют в G тогда и только тогда, когда G редуктивная группа. Если G связна, то объединение всех ее Б. п. совпадает с ней самой и всякая параболич. подгруппа совпадает со своим нормализатором в G. В этом случае Б. п. является максимальной среди всех (а не только алгебраических и связных) разрешимых подгрупп группы G. Однако, вообще говоря, могут существовать максимальные разрешимые подгруппы в G, не являющиеся Б. п. Коммутант Б. п. В совпадает с ее унипотентной частью В_u, а нормализатор В_u в G совпадает с В. Если характеристика основного поля равна 0, а 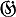есть алгебра Ли группы G, то подалгебра 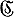алгебры 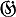, являющаяся алгеброй Ли Б. п. В группы G часто наз. Бореля подалгеброй (или борелевской подалгеброй) в 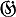. Подалгебры Бореля в алгебре 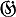- это в точности ее максимальные разрешимые подалгебры. Для k-определенной алгебраич. группы G над произвольным полем k обобщением Б. п. над k являются минимальные параболич. k - определенные подгруппы, к-рые сопряжены посредством элементов из G_k (см. [2]).

Лит. : [1] Воrеl А., «Аnn. Math. », 1956, v. 64, № 1, p. 20-82; [2] Борель А., Титс Ж., «Математика», 1967, т. 11, № 1, С. 43-111.

В. П. Платонов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.