БОРЕЛЯ МЕТОД СУММИРОВАНИЯ

Расстановка ударений: БОРЕ`ЛЯ МЕ`ТОД СУММИ`РОВАНИЯ

БОРЕЛЯ МЕТОД СУММИРОВАНИЯ - один из методов суммирования функциональных рядов, предложенный Э. Борелем [1]. Пусть дан числовой ряд

(*)

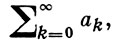
S_n - его частные суммы и S - действительное число. Ряд (*) суммируется методом Бореля (B-методом) к числу S, если

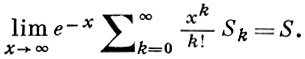
Существует интегральный метод суммирования Бореля, В'-метод: если

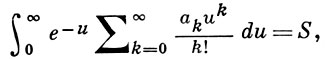
то говорят, что ряд (*) суммируется В'-методом к числу s. Условия, при к-рых B-метод и B'-метод равносильны, см. [2], с. 229. В-метод возник в связи с аналитич. продолжением функции, регулярной в точке. Пусть

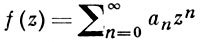
регулярна в точке О и С - совокупность всех ее особых точек. Через каждую точку Р ∈ С проведем отрезок ОР и прямую L_p, проходящую через точку Р перпендикулярно к ОР. Совокупность точек, лежащих по одну сторону с О от каждой из прямых L_p, обозначим П. Тогда граница Г области П наз. многоугольником Бореля функции f(z), а область П - его внутренней областью. Имеет место теорема: ряд

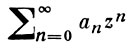
суммируется В'-методом в области П и не суммируется в области П*-дополнении к П (см. [2]).

Лит. : [1] Вorel Е., «Аnn. scient. École norm. supér. », 1899, ser. 3, t. 16, p. 9-136; [2] Харди Г., Расходящиеся ряды, пер. с англ., М., 1951.

А. А. Захаров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.