БОРЕЛЯ МЕРА

Расстановка ударений: БОРЕ`ЛЯ МЕ`РА

БОРЕЛЯ МЕРА множеств - неотрицательная функция μ подмножеств топологич. пространства X, обладающая следующими свойствами: 1) область ее определения есть σ-алгебра ℬ борелевских множеств из X, т. е. наименьший класс подмножеств из X, содержащий открытые множества и замкнутый относительно теоретико-множественных операций, производимых в счетном числе; 2) 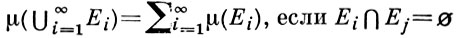при i ≠ j, то есть μ счетно аддитивна. Б. м. μ наз. регулярной, если

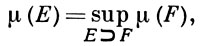
где F принадлежит классу ℱ замкнутых подмножеств из X. Нередко изучение Б. м. связывают с изучением мер Бэра, к-рые отличаются от Б. м. лишь областью их определения: они определены на наименьшей σ-алгебре ℬ '₀, относительно к-рой измеримы все непрерывные функции на X. Б. м. μ (соответственно мера Бэра ν) наз. τ-гладкой, если μ (F_α) для любой сети {F_α} замкнутых множеств, удовлетворяющей условию F_α ↓ ∅ (соответственно ν (Z_α) ↓ 0 для любой сети {Z_α} множеств, являющихся нулями непрерывных функций, при условии, что Z_α ↓ ∅. Б. м. μ (соответственно мера Бэра ν) наз. плотно й, если μ (E) = sup_{E ⊃ K ∈ K} μ (K), где K-класс компактных подмножеств из X (соответственно ν (E) = sup_{E ⊃ K ∈ K} ν * (K), где ν *(K) = inf_{K ⊂ E0 ∈ ℬ0} ν (E₀)). Плотность и τ-гладкость являются ограничениями, обеспечивающими дополнительную гладкость мер, и часто выполняются в конкретных ситуациях. При определенных условиях меры Бэра могут быть продолжены до Б. м. Напр., если X вполне регулярно и хаусдорфово, то всякая τ-гладкая (плотная) конечная мера Бэра может быть продолжена до регулярной τ-гладкой (плотной) конечной Б. м. При изучении мер на локально компактных пространствах Б. м. (соответственно мерами Бэра) наз. иногда меры, определенные на σ-кольце множеств, порожденном компактными (соответственно компактными G_δ) множествами, и конечные на компактных множествах. Мерой Бореля на прямой часто наз. меру, определенную на борелевских множествах и такую, что ее значение на произвольном отрезке равно длине этого отрезка.

Лит. : [1] Варадарайн В. С., «Матем. сб. », 1961, т. 55, № 1, с. 35-100; [2] Халмош П., Теория меры, пер. с англ., М., 1953; [3] Неве Ж., Математические основы теории вероятностей, пер. с франц., М., 1969.

В. В. Сазонов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.