БОРДИЗМ

Расстановка ударений: БОРДИ`ЗМ

БОРДИЗМ, бордантность, - термин, употребляющийся самостоятельно или в составе стандартных словосочетаний в нескольких родственных смыслах (почти во всех из них вместо Б. раньше говорили о кобордизмах; старая терминология тоже сохранилась).

Простейший вариант: два гладких замкнутых n-мерных многообразия М₀ и M бордантны (соограничивают, или внутренне гомологичны), если существует гладкое компактное (n + 1)-мерное многообразие W («пленка»), край к-рого состоит из двух многообразий N₀ и N, диффеоморфных, соответственно, М₀ и М посредством нек-рых диффеоморфизмов

g₀ : N₀ → M₀ и g: N → M.

Совокупность многообразий, бордантных друг другу, наз. классами бордизмов, а тройку (W, М₀, М) иногда наз. бордизмом [точнее было бы говорить о пятерке (W, М₀, М, g₀, g)]. Множество классов Б. n-мерных многообразий образует абелеву группу 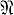_n относительно несвязного объединения. Нулем в ней служит класс Б., состоящих из многообразий М, к-рые являются границей нек-рого многообразия W [формально говорят отройке (W, М₀, М) с пустым М₀ ; другие названия: М-ограничивающее многообразие, М - внутренне гомологично, или бордантно нулю]. Элементом 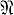_n, обратным данному классу Б., является сам этот класс (т. к. М ∪ М диффеоморфно границе прямого произведения М × [0, 1]). Прямая сумма 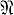_* групп 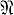_n является коммутативным градуированным кольцом, умножение в к-ром индуцировано прямым произведением многообразий, с единицей, заданной классом Б. точки.

Более сложные варианты - Б. гладких замкнутых многообразий с дополнительной структурой. Напр., два ориентированных многообразия М₀ и М ориентированно бордантны, если они бордантны в прежнем смысле, причем «пленка» W ориентирована, и (в прежних обозначениях) ориентация, индуцированная ориентацией W на N₀ и N (как на частях края), переходит при диффеоморфизмах g₀ и g, соответственно, в исходную ориентацию М и в ориентацию, противоположную исходной ориентации М₀ . В этом случае говорят об ориентированных бордизмах, а если надо подчеркнуть отличие от них Б. в предыдущем смысле, последние наз. неориентированными. 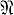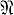Аналогично _n и _* вводятся группы ориентированных Б. Ω_n и кольцо Ω_* = Σ Ω_n .

Исторически первый пример - Б. оснащенных многообразий, введенный в 1938 Л. С. Понтрягиным, к-рый показал, что классификация этих Б. эквивалентна вычислению гомотопич. групп сфер π_i (Sⁿ), и таким путем смог найти π_{n + 1} (Sⁿ) и π_{n + 2} (Sⁿ) (подробное изложение его исследований см. в более поздней публикации [2], элементарное введение - в [4]). Неориентированные и ориентированные Б. были введены в 1951-53 В. А. Рохлиным (см. [3]), вычислившим 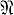_n и Ω_n для n ≤ 4. Ранее Л. С. Понтрягин [1] доказал, что если два многообразия бордантны, то у них совпадают характеристич. числа (числа Штифеля-Уитни в неориентируемом случае, числа Штифеля-Уитни и числа Понтрягина - в ориентируемом). (Впоследствии оказалось, что обратное тоже верно.)

Использование в теории Б. современных методов алгебраич. топологии началось с вышедшей в 1954 работы Р. Тома (см. [5], [6]), переоткрывшего применительно к неориентированным и ориентированным Б. связь между Б. и нек-рыми гомотопич. задачами. Так, группа изоморфна группе π_{n + r} (ТВО (r)) с достаточно большим r; здесь ТВО (r) - Тома пространство универсального векторного расслоения со структурной группой О (r). Эта связь позволила Р. Тому полностью вычислить кольцо 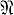_* и существенно продвинуть изучение Ω_*, впоследствии завершенное другими учеными. Напр., 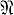_* оказалось кольцом многочленов над полем вычетов mod 2 от образующих x_i размерности i, где i пробегает все положительные числа, не равные 2^s - 1, s ≥ 1; известна геометрич. реализация этих образующих (т. е. указаны конкретные многообразия, классы Б. к-рых суть x_i (см. [7]).

Другие варианты Б. многообразия с дополнительной структурой - очень важные Б. квазикомплексных многообразий (наз. также унитарными Б.) (см. [8], [9]), Б. многообразий, на к-рых действует группа преобразований (см. [10]); имеются также варианты несколько иного рода (для кусочно линейных или топологич. многообразий, для комплексов Пуанкаре) и т. д. (см. [11]). Особое положение занимают бордизмы слоений и h-бордизмы (ранее наз. J-эквивалентностями); последние служат для связи дифференциальной и гомотопич. топологии [12].

Дальнейшее развитие теории Б. связано с группами бордизмов топологич. пространства X (короче, Б. пространства X, см. [13]). Они определяются для различных вариантов Б. (ниже приводится простейший случай). Сингулярным n-мерным (под) многообразием пространства X наз. пара (Мⁿ, f), где Мⁿ - замкнутое гладкое многообразие, f: Мⁿ → Х - непрерывное отображение. Две такие пары (М₀, f₀), (Мⁿ, f) бордантны, если M₀ и M бордантны в обычном смысле и (в прежних обозначениях) существует такое непрерывное отображение h: W → Х, что hg^{- 1}₀ = f₀, hg^{- 1} = f₀ . (Если отождествить M₀ и М с N₀ и N, то можно просто сказать, что отображение h индуцирует заданные отображения М₀ и M в X). Классы Б. сингулярных многообразий пространства X образуют n-мерную группу Б. 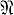_n (X) этого пространства (групповая операция порождена объединением многообразий).

Если X - многообразие размерности > 2n, то элементы 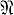_n (Х) наглядно представляются подмногообразиями, как и соответствующие «пленки», в этом отношении Б. пространства X близки к первоначальным попыткам введения гомологии. Если X - точка, то 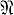_n (Х) сводится к прежнему 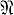_n . Отображению φ : Х → Y соответствуют гомоморфизмы φ_n : 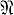_n (X) → 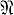_n (Y), порожденные переходом от сингулярных многообразий (M, f) к (M, φ f). Функтор, сопоставляющий каждому пространству X группы 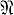_n (X) и отображению φ - отображения φ_n, является обобщенной теорией гомологии. В данном случае она сводится к обычным гомологиям, а именно, для любого клеточного полиэдра X

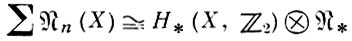
(справа стоит тензорное произведение градуированных модулей над ℤ₂), но для других Б. (ориентированных и т. д.) это, вообще говоря, не так. Многие обобщенные теории гомологии могут быть получены посредством так наз. Б. с особенностями (см. [14]).

Наряду с Б. пространства X существуют двойственные им обобщенные когомологий. Введение этих функторов обобщенных гомологий и когомологий сделало желательным то изменение терминологии, о к-ром говорилось в начале статьи: термин «кобордизм» резервируется для обобщенных когомологий, двойственных Б.

Лит. : [1] Понтрягин Л. С., «Матем. сб. », 1947, т. 21, № 2, с. 233-84; [2] его же, Гладкие многообразия и их применение в теории гомотопий, 2 изд., М., 1976; [3] Pохлин В. А., «Успехи матем. наук», 1959, т. 14, № 4, с. 3-20; [4] Милнор Дж., Уоллес А., Дифференциальная топология, пер. с англ., М., 1972; [5] Том Р., в кн. : «Расслоенные пространства и их приложения» (сб. переводов), М., 1958, с. 293-351; [6] Милнор Дж., «Математика», 1964, т. 9, № 4, с. 3-40; [7] Dоld A., «Math. Z. », 1956, Bd 65, S. 25-35; [8] Milnor J., «Amer. J. math. », 1960, v. 82, p. 505-21; [9] Новиков С. П., «Матем. сб. », 1962, т. 57 [99], с. 406-42; [10] Коннер П., Флойд Э., Гладкие периодические отображения, пер. с англ., М., 1969; [11] Стонг Р., Заметки по теории кобордизмов, пер. с англ., М., 1973; [12] Милнор Дж., Теорема об h-кобордизме, пер. с англ., М., 1969; [13] Atiуah М., «Рrос. Camb. Phil. Soc. », 1961, v. 57, pt 2, p. 200-8; [14] Baas N.. «Math. Scand. », 1973, v. 33, №2, p. 279-302, 302-13.

Д. В. Аносов, M. И. Войцеховский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.