БОРА-ФАВАРА НЕРАВЕНСТВО

Расстановка ударений: БО`РА-ФА`ВАРА НЕРА`ВЕНСТВО

БОРА-ФАВАРА НЕРАВЕНСТВО - неравенство, возникшее в связи с задачей X. Бора [1] об ограниченности на всей действительной оси первообразной почти периодич. функции. Окончательный вид этому неравенству дал Ж. Фавар [2], существенно дополнивший исследования X. Бора и рассмотревший для фиксированных натуральных чисел гига произвольную периодич. функцию

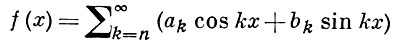
с непрерывной производной f^(r) (х). Б.-Ф. н. принчто наз. неравенство

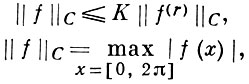
с наилучшей константой К = К(n, r):

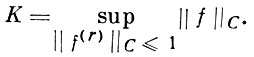
Б.-Ф. н. тесно связано с неравенством для наилучших приближений функции и ее r-й производной тригонометрич. полиномами порядка не выше n и с поперечниками Колмогорова класса дифференцируемых функций.

Лит. : [1] Bohr Н., «С. r. Acad. sci. », 1935, t. 200, № 15, p. 1276-7; [2] Favard J., «Bull. sci. math. », 1937, t. 61, p. 243-56; [3] Axиeзep H. И., Лекции по теории аппроксимации, 2 изд., M., 1965.

Л. В. Тайков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.