БОННЕ ТЕОРЕМА

Расстановка ударений: БО`ННЕ ТЕОРЕ`МА

БОННЕ ТЕОРЕМА - 1) Б. т. о существовании и единственности поверхности с заданными первой n второй квадратичными формами [1]: пусть заданы две квадратичные формы:

Е du² + 2F dudv + G dv², L du² + 2M dudv + N dv²,

первая из к-рых положительно определенная и коэффициенты этих форм удовлетворяют уравнениям Гаусса (см. Гаусса теорема) и Петерсона-Кодацци уравнениям; тогда существует, и притом единственная с точностью до положения в пространстве поверхность, для к-рой эти формы являются соответственно первой и второй квадратичными формами.

2) Б. т. о диаметре овальной поверхности: если кривизна овальной поверхности во всех ее точках больше или равна 1/A², то внешний диаметр этой поверхности меньше π А; эта оценка не может быть улучшена. Установлена О. Бонне (О. Bonnet, 1855).

А. Б. Иванов.

3) Б. т. о среднем значении, вторая теорема о среднем значений [2]: пусть f(x), φ (х) интегрируемые функции на отрезке [а, b] и пусть φ (х) - положительная убывающая функция от х; тогда найдется такое число ξ на отрезке [а, b], для к-рого имеет место равенство

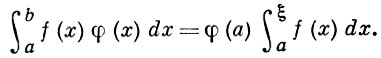
Если от φ (x) требовать только монотонности, то Б. т. утверждает, что на [а, b] найдется такая точка ξ, что выполняется

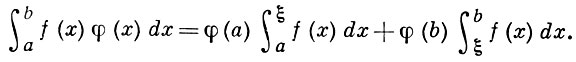
Лит. : [1] Воnnеt О., «J. Ecole polyt. », 1865, t. 24, p. 204-230; 1867, t. 25, p. 1-151; [2] его же, «J. math. », 1849, t. 14, p. 249-56.

Т. Ю. Попова.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.