БОЛЯ ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ

Расстановка ударений: БО`ЛЯ ПОЧТИ` ПЕРИОДИ`ЧЕСКИЕ ФУ`НКЦИИ

БОЛЯ ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ - класс функций, определяемый тем свойством, что они могут быть равномерно приближены на всей действительной оси посредством обобщенных тригонометрич. полиномов вида:

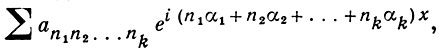
где n₁, ..., n_k - любые целые, а α₁, ..., α_n - заданные действительные числа. Этот класс функций был впервые рассмотрен и подробно исследован П. Болем [1]. Класс Б. п. п. ф. содержит в себе класс непрерывных 2π - периодических функций, и содержится в классе Бора почти периодических функций. П. Боль указал ряд необходимых и достаточных условий почти периодичности функции. В частности, всякая функция вида:

f(x) = f₁ (x) + f₂ (x) + ... + f_k (х), где каждая из функций f₁ (x), f₂ (x), ..., f_k (x) непрерывна и периодична (периоды их могут быть различны), является Б. п. п. ф.

Лит. : [1] Воhl P., Ueber die Darstellung von Functionen einer Variabeln durch trigonometrische Reihen mit mehreren einer Variabeln proportionalen Argumenten, Dorpat, 1893; [2] Воhl P., «J. reine und angew. Math. », 1906, Bd 131, S. 268-321; [3] Левитан Б. M., Почти-периодические функции, 1953.

Е. А. Бредихина.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.