БОЛЬШОЕ РЕШЕТО

Расстановка ударений: БОЛЬШО`Е РЕШЕТО`

БОЛЬШОЕ РЕШЕТО - метод, разработанный Ю. В. Линником в 1941 и позволяющий высеивать последовательности с возрастающим числом выбрасываемых вычетов. Сущность Б. р. заключается в следующем. Пусть задана последовательность целых положительных чисел n₁, ..., n_z, не превосходящих N, простое число р ≤ √N и вычет l, 0 ≤ l ≤ p - 1. Пусть

Из статистич. соображений, к-рые могут быть строго обоснованы с помощью основной идеи кругового метода, следует, что Q(р, l) > 0 для почти всех р и, соответственно, для почти всех l. Пусть А - количество таких р, а B = B(р) - количество соответствующих l.

Ю. В. Линник доказал, что

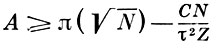
и

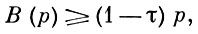
где C > 0 - константа, а τ ∈ (0, 1), и вывел теорему о том, что количество простых чисел из сегмента [N^ε, N], для к-рых нарушается гипотеза И. М. Виноградова о наименьшем квадратичном невычете (см. Виноградова гипотезы), может быть только конечным (зависящим от ε).

Имеются усовершенствования метода Б. р., при этом рассматриваются оценки величины Q(р, l) в среднем. Лучший результат принадлежит Э. Бомбьери (Е. Воmbieri, 1965):

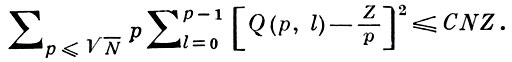
Наиболее значительный вклад в современную аналитич. теорию чисел метод Б. р. дал в сочетании с плотностным методом, что привело к доказательству теоремы Виноградова-Бомбьери (1965) - усредненного асимптотич. закона простых чисел в прогрессиях. Эта и другие аналогичные теоремы о среднем нашли широкое применение при решении ряда известных задач теории чисел, заменяя во многих случаях Римана обобщенную гипотезу.

Лит. : [1] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [2] Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., М., 1971; [3] Монтгомери Г., Мультипликативная теория чисел, пер. с англ., М., 1974.

Б. М. Бредихин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.