БОЛЬШИХ ЧИСЕЛ УСИЛЕННЫЙ ЗАКОН

Расстановка ударений: БОЛЬШИ`Х ЧИ`СЕЛ УСИ`ЛЕННЫЙ ЗАКО`Н

БОЛЬШИХ ЧИСЕЛ УСИЛЕННЫЙ ЗАКОН - одна из форм больших чисел закона (в его общем понимании), утверждающая, что при определенных условиях с вероятностью единица происходит неограниченное сближение средних арифметических последовательности случайных величин с нек-рыми постоянными величинами. Точнее, пусть

X₁, ..., X_n,... (1)

- последовательность случайных величин и S_n = X₁ + ... + X_n . Говорят, что последовательность (1) удовлетворяет Б. ч. у. з., если существует такая последовательность постоянных А_n, что вероятность соотношения

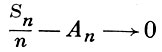
(2)

(при n → ∞) равна 1. Другая формулировка, равносильная предыдущей, такова: последовательность (1) удовлетворяет Б. ч. у. з., если при любом ε > 0 вероятность одновременного выполнения всех неравенств

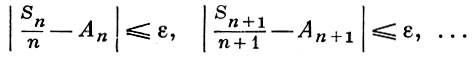
(3)

стремится к 1 при n → ∞. Таким образом, здесь рассматривается поведение всей последовательности сумм в целом, в то время как в обычном законе больших чисел речь идет лишь об отдельных суммах. Если последовательность (1) удовлетворяет Б. ч. у. з., то она удовлетворяет и обычному закону больших чисел с теми же самыми А_n, т. е.

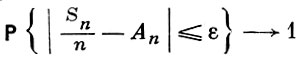
(4)

(при любом ε > 0 и n → ∞). Обратное может быть неверно. Напр., если случайные величины (1) независимы и принимают при n ≥ 16 два значения 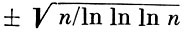с вероятностью 1/2 каждое, то для них выполняется закон больших чисел (4) с А_n = 0, но ни при каких А_n не выполняется Б. ч. у. з. (2). Заранее существование таких примеров совсем не очевидно, т. к. хотя вообще сходимость по вероятности слабее сходимости с вероятностью 1, тем не менее, напр., для рядов из независимых случайных величин оба вида сходимости равносильны.

Б. ч. у. з. был впервые сформулирован и доказан Э. Борелем [1] для схемы Бернулли (в теоретико-числовой интерпретации; см. Бореля усиленный закон больших чисел). Частные случаи схемы Бернулли возникают при разложении взятого наудачу (с равномерным распределением) действительного числа ω из отрезка (0, 1) в бесконечную дробь по к.-л. основанию (см. Бернулли испытания). Так, в двоичном разложении

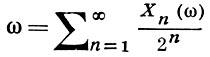
последовательные знаки Х_n (ω) принимают два значения 0 и 1 с вероятностью 1/2 каждое и являются независимыми случайными величинами. Сумма 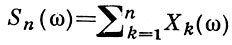равна числу единиц среди первых n знаков двоичного разложения, a S_n (E)/n - их доле. В то же время S_n может рассматриваться как число «успехов» в схеме Бернулли с вероятностью «успеха» (появление 1), равной 1/2. Э. Борель доказал, что доля единиц S_n (ω)/n стремится к 1/2 для пояти всех со из отрезка (0, 1). Аналогично, при разложении ω по основанию 10 можно назвать «успехом» появление к.-л. одной из цифр 0, 1, 2, ..., 9 (напр., цифры 3). При этом получается схема Бернулли с вероятностью успеха 1/10, и частота появления выбранной цифры среди первых n знаков десятичного разложения стремится к 1/10 для почти всех ω из отрезка (0, 1). Э. Борель отметил также, что частота появления любой фиксированной группы r цифр стремится для почти всех ω к 1/10^r (см. Нормальное число).

Ф. Кантелли [2] дал достаточные условия Б. ч. у. з. для независимых случайных величин Х_n в терминах вторых и четвертых центральных моментов слагаемых (схема Бернулли охватывается этими условиями). Вводя обозначение

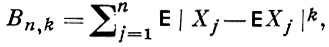
условию Кантелли можно придать вид

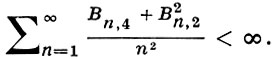
Доказательства Э. Бореля и Ф. Кантелли основаны на следующем соображении. Пусть для нек-рой последовательности положительных чисел ε_n → 0 (при n → ∞)

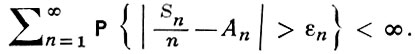
(5)

Тогда по Бореля-Кантелли лемме с вероятностью 1 осуществляется лишь конечное число событий, стоящих под знаком вероятности в (5). Поэтому с вероятностью 1 для всех достаточно больших n

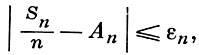
т. е. имеет место (3). Э. Борель оценивал члены ряда (5) по теореме Муавра-Лапласа, а Ф. Кантелли - по неравенству Чебышева с четвертыми моментами.

Дальнейшее расширение условий приложимости Б. ч. у. з. было осуществлено А. Я. Хинчиным и А. Н. Колмогоровым. А. Я. Хинчин [3], [4] ввел самый термин «усиленный закон больших чисел» и дал достаточное условие Б. ч. у. з. с a_n = E (S_n /n) (применимое и к зависимым величинам). Обозначая через r_{i, k} коэффициент корреляции между X_i и X_k и полагая

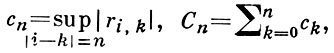
можно записать условие Хинчина в форме: В_{n, 2} С_n = O(n^{2 - δ}) для нек-рого δ > 0. В действительности из доказательства А. Я. Хинчина вытекает значительно более сильное утверждение.

В случае независимых слагаемых наиболее известными являются условия приложимости Б. ч. у. з., установленные А. Н. Колмогоровым: достаточное (1930) - для величин с конечными дисперсиями и необходимое и достаточное (1933) - для одинаково распределенных величин (заключающееся в существовании математич. ожидания величин X_i). Теорема Колмогорова для случайных величин (1) с конечными дисперсиями утверждает, что из условия

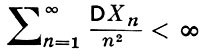
(6)

вытекает приложимость к последовательности (1) Б. ч. у. з. с A_n = E(S_n /n). В терминах дисперсий условие (6) оказывается наилучшим в том смысле, что для любой последовательности положительных чисел b_n с расходящимся рядом ∑ b_n /n² можно построить последовательность независимых случайных величин Х_n с D X_n = b_n, не удовлетворяющую Б. ч. у. з. Область применения условия (6) (как, впрочем, и ряда других условий Б. ч. у. з. для независимых величин) может быть расширена на основе следующего замечания. Пусть m_n - медиана Х_n . Сходимость ряда

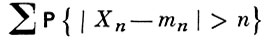
необходима для Б. ч. у. з. Из леммы Бореля-Кантелли вытекает, что с вероятностью 1, начиная с нек-рого номера, |X_n - m_n | < n. Поэтому при изучении условий приложимости Б. ч. у. з. можно сразу ограничиться случайными величинами, удовлетворяющими последнему условию.

В доказательствах А. Я. Хинчина и А. Н. Колмогорова вместо сходимости ряда (5) устанавливается сходимость ряда

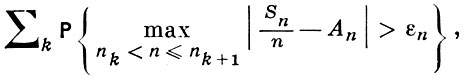
где n_k = 2^k . При этом А. Я. Хинчин привлекал, по существу, нек-рые идеи из теории рядов по ортогональным системам функций, а А. Н. Колмогоров использовал носящее его имя неравенство для максимумов сумм случайных величин.

Для независимых случайных величин можно дать необходимое и достаточное условие Б. ч. у. з. Полагая

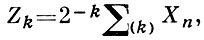
где сумма ∑_(k) распространена на те n, для к-рых 2^k < n ≤ 2^{k + 1}, это условие можно записать в виде: при любом ε > 0

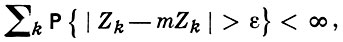
(7)

где mZ_k - медиана Z_k (см. [6]). Из (7) при дополнительных ограничениях можно получить условия, выраженные через характеристики отдельных слагаемых. Если, напр., 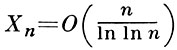или если все Х_n распределены по нормальному закону, то условие (7) равносильно следующему: при любом ε > 0

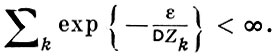
(8)

Здесь, в силу независимости X_i,

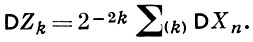
Известны условия применимости Б. ч. у. з. к марковским цепям и процессам и стационарным процессам (см. [7]). Напр., метод Хинчина, примененный к стационарным в широком смысле последовательностям Х_n с корреляционной функцией R (n), приводит к следующему утверждению: если ряд 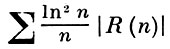сходится, то 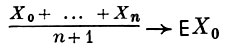с вероятностью 1. Для стационарных в узком смысле процессов Б. ч. у. з. иногда толкуют, понимая под этим утверждение, что с вероятностью 1 существует предел

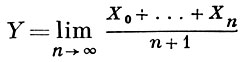
(случайная величина Y равна условному математич. ожиданию Х₀ по отношению к σ - алгебре множеств, инвариантных относительно сдвига; с вероятностью 1 величина Y постоянна и равна ЕХ₀ только для метрически транзитивных процессов). В указанной форме Б. ч. у. з. есть не что иное, как Биркгофа эргодическая теорема.

Существуют варианты Б. ч. у. з. для случайных векторов в нормированных линейных пространствах [9]. В качестве исторически первого примера можно привести теорему Гливенко-Кантелли о сходимости эмпирической функции распределения к теоретической.

Представление об отклонениях S_n /n от А_n дает повторного логарифма закон.

Лит. : [1] Вorel Е., «Rend. Circolo mat. Palermo», 1909, v 27, p. 247-71; [2] Сantelli F. P., «Atti Accad. naz. Lincei», 1917, v. 26, p. 39-45; [3] Xинчин А. Я., Основные законы теории вероятностей, М., 1927; [4] его же, «С. r. Acad. sci. », 1928, t. 186, p. 285-7; [5] Колмогоров A. H., «С. r. Acad. sci. », 1930, t. 191, p. 910-2; [6] Пpоxоpов Ю. В «Изв. АН СССР. Сер. матем. », 1950, т. 14, с. 523-36; [7] Дуб Дж., Вероятностные процессы, пер. с англ., М., 1956; [8] Петров В. В., Суммы независимых случайных величин, М., 1972; [9] Гренандер У., Вероятности на алгебраических структурах, пер. с англ., М., 1965.

Ю. В. Прохоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.