БОЛЬШИХ ОТКЛОНЕНИЙ ВЕРОЯТНОСТИ

Расстановка ударений: БОЛЬШИ`Х ОТКЛОНЕ`НИЙ ВЕРОЯ`ТНОСТИ

БОЛЬШИХ ОТКЛОНЕНИЙ ВЕРОЯТНОСТИ - вероятности вида

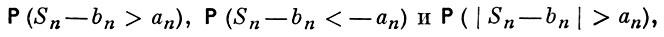
где

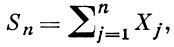
{Х_j} - последовательность независимых случайных величин, а {а_n} и {b_n} - две последовательности чисел такие, что 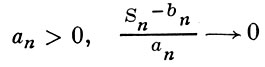по вероятности.

Если случайные величины Х₁, Х₂ ... имеют одинаковое распределение с математич. ожиданием, равным нулю, и конечной дисперсией σ², то можно положить b_n = 0 и a_n = х_n σ √n, где х_n → + ∞ при n → ∞. Особенно большое значение имеют Крамера теорема и ее усиления.

В случаях, когда необходимо иметь гарантированные оценки для Б. о. в., пользуются неравенствами типа Чебышева неравенств - это так наз. показательные оценки для Б. о. в. Напр., если случайные величины X_j независимы, ЕХ_j = 0, ЕХ²_j = σ²_j, |X_j | ≤ L с вероятностью 1, B²_n = σ²₁ + ... + σ²_n, и a = хL/В_n, то при всех х ̥ 0 верна оценка

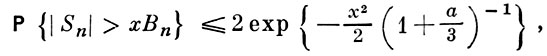
правая часть к-рой экспоненциально убывает с ростом х.

Лит. : [1] Лоэв М., Теория вероятностей, пер. с англ., М 1962; [2] Петров В. В., Суммы независимых случайных величин, М., 1972; [3] Ибрагимов И. А., Линник Ю. В., Независимые и стационарно связанные величины, М., 1965; [4] Прохоров Ю. В., в кн. : Итоги науки и техники, т. 10, М., 1972, с. 5-24; [5] Юринский В. В., «Теория вероятностей и её применения», 1974, т. 19, в. 1, с. 152-153.

В. В. Петров, В. В. Юринский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.