БОЛЬЦМАНА УРАВНЕНИЕ

Расстановка ударений: БО`ЛЬЦМАНА УРАВНЕ`НИЕ

БОЛЬЦМАНА УРАВНЕНИЕ - уравнение кинетич. теории газов, предложенное Л. Больцманом (L. Boltzmann) для определения одночастичной функции распределения идеального одноатомного газа (см. [1]). В безразмерных переменных Б. у. имеет вид:

(*)

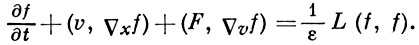
Здесь f(x, v, t) - плотность функции распределения числа частиц в фазовом пространстве x⊗ v, х - трехмерная пространственная координата, v - скорость, t - время, F - плотность внешних массовых сил, ε - безразмерный параметр (пропорциональный отношению среднего расстояния, к-рое частицы пролетают без столкновений, к характерному масштабу рассматриваемых явлений). Оператор столкновений L в простейшем случае имеет следующий вид:

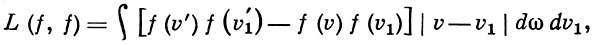
где v₁ и v - скорости молекул до столкновения, v'₁ и v' - скорости молекул после столкновения, dω - элемент площади в плоскости, перпендикулярной вектору v₁ - v.

При выводе Б. у. предполагается, что эволюция функции f(x, v, t) определяется ее значением в данный момент времени t и парными столкновениями между молекулами газа, причем время взаимодействия двух молекул газа при столкновении много меньше того времени, в течение к-рого они двигаются как свободные частицы. С математич. точки зрения вывод Б. у. заключается в определенном алгоритме построения оператора L на основе известного закона движения двух сталкивающихся друг с другом молекул газа.

В уравнении (*) область изменения переменной t - полупрямая t ≥ 0, область изменения v - все пространство R³, область изменения х - подобласть Ω в R³ (Ω может и совпадать с R³). По физич. смыслу функция f(x, v, t) должна быть неотрицательной и такой, что

∫ f (х, v, t) v² dv < ∞.

Простейшее граничное условие на dΩ имеет следующий вид:

f (v - 2n (n, v); х; t) = f (v, х, t), x ∈ ∂Ω, v ∈ R³,

где n - нормаль к dΩ. Имеется несколько различных точных постановок задачи Коши для уравнения (*), однако ни для одной из них не доказано существование в целом решения уравнения (*) при естественных с физич. точки зрения предположениях об операторе L.

Лит. : [1] Больцман Л., Лекции по теории газов, пер. с нем., М., 1956; [2] Боголюбов Н. Н., Избр. труды, т. 2, К., 1970; [3] Чепмен С. и Каулинг Т. Д., Математическая теория неоднородных газов, пер. с англ., М., 1960.

А. А. Арсеньев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.