БОЛЬЦА ЗАДАЧА

Расстановка ударений: БО`ЛЬЦА ЗАДА`ЧА

БОЛЬЦА ЗАДАЧА - одна из основных задач классического вариационного исчисления на условный экстремум при наличии ограничений типа равенств - сформулирована О. Больца (О. Bolza) в 1913. Б. з. состоит в том, чтобы минимизировать функционал

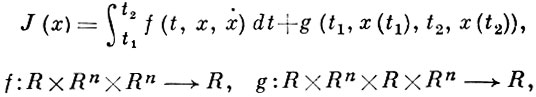
при наличии дифференциальных ограничений типа равенства:

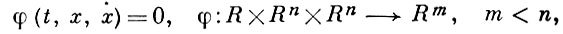
и граничных условий:

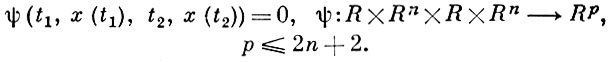
При g ≡ 0 Б. з. наз. Лагранжа задачей, при f ≡ 0 и р < 2n + 2 - Майера задачей. Особенностью Б. з. является смешанный характер функционала, к-рый представляет собой сумму интегрального функционала и функции от концов. С принципиальной точки зрения Б. з. равносильна задаче Лагранжа и приводится к ней, если положить

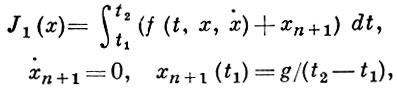
а также - задаче Майера, если положить

Выбор той или иной формы задачи, а также той топологии, в к-рой затем рассматривается эта задача, диктуется соображениями удобства или конкретной целесообразности. В теории оптимального управления чаще рассматриваются задачи в форме Майера, в классическом вариационном исчислении - в форме Лагранжа. Наиболее употребительна топология пространства С¹ непрерывно дифференцируемых функций. Для получения необходимых или достаточных условий экстремума надо накладывать требования гладкости на входящие в определения задачи функции f и g и отображения φ и ψ, а также требования о регулярности отображений φ и ψ, заключающиеся в том, что матрицы должны иметь максимальный ранг р и m соответственно. Для того чтобы вектор-функция x(t) доставляла экстремум в Б. з. (аналогично в задачах Лагранжа и Майера), необходимо, чтобы вдоль нее удовлетворялись Эйлера уравнения и Вейерштрасса условие относительно Лагранжа функции, составленной по входящим в задачу данным с Лагранжа множителями, а также Якоби условие и трансверсальности условия.

В приведенной формулировке Б. з. использованы обозначения, характерные для теории оптимального управления. В классическом вариационном исчислении Б. з. формулируют, используя другие обозначения:

Лит. : [1] Блисс Г. А., Лекции но вариационному исчислению, пер. с англ., М., 1950.

И. Б. Вапнярский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.