БОКСА ИНТЕГРАЛ

Расстановка ударений: БО`КСА ИНТЕГРА`Л

БОКСА ИНТЕГРАЛ - одно из обобщений интеграла Лебега, предложенных А. Данжуа (A. Denjoy, 1919), подробно изученное Т. Дж. Боксом (Т. J. Boks, 1921). Действительная функция f(x) на отрезке [а, b] периодически (с периодом b - а) продолжается на всю прямую. Для произвольного разбиения а = х₀ < х₁ <... < х_n = b отрезка [а, b], произвольного набора точек ξ¯ = {ξ_i}ⁿ₀, ξ_i ∈ [x_{i - 1}, x_i ] и произвольного t строится сумма

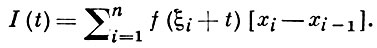
Если I (t) при ρ = max (x_i - x_{i - 1}) → 0 сходится по мере к определенному пределу I, то число I наз. интегралом Бокса (B - интегралом) от f (х) по [а, b]. Таким образом, Б. и. есть интеграл риманова типа и является также обобщением интеграла Римана.

Б. и. существенно расширяет интеграл Лебега: всякая суммируемая функция Р-интегрируема и эти интегралы совпадают, в то время как существуют несуммируемые Р-интегрируемые функции; в частности, если g - сопряженная функция к суммируемой функции f, то она Р-интегрируема и коэффициенты ряда, сопряженного к ряду Фурье от f, есть коэффициенты соответствующего ряда Фурье (в смысле Р-интегрирования) от g (А. Н. Колмогоров). Дальнейшего развития теория Б. и. не получила, т. к. для интегрирования функций, сопряженных к суммируемым, более удобным оказался А-интеграл.

Лит. : [1] Boks T. J., "Rend. Circolo mat. Palermo", 1921, v. 45, p. 211-264; [2] Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1-2, М., 1965.

И. А. Виноградова.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.