БОЗЕ-ЭЙНШТЕЙНА СТАТИСТИКА

Расстановка ударений: БОЗЕ`-ЭЙНШТЕ`ЙНА СТАТИ`СТИКА

БОЗЕ-ЭЙНШТЕЙНА СТАТИСТИКА, Бозе статистика, - квантовая статистика, применяемая к системам тождественных частиц с целым спином (0, 1, 2,... в единицах ħ = 1, 05 ⋅ 10^{- 27} эрг ⋅ сек). Предложена Ш. Бозе (S. Bose) и А. Эйнштейном (A. Einstein) в 1924. Согласно этой статистике, в каждом квантовом состоянии может находиться произвольное число частиц. В. Паули (W. Pauli) доказал, что тип квантовой статистики однозначно связан со спином частиц, так как совокупности частиц с целым спином подчиняются Б.-Э. с, а с полуцелым спином - Ферми-Дирака статистике.

Состояние системы многих частиц в квантовой механике определяется волновой функцией, к-рая в случае тождественных частиц может быть либо симметричной по отношению к перестановкам любой пары частиц (для частиц с целым спином), либо антисимметричной (для частиц с полуцелым спином). Для системы частиц, подчиняющихся Б.-Э. с, состояния описываются симметричными волновыми функциями, что является другой, эквивалентной формулировкой Б.-Э. с. Системы из большого числа частиц, подчиняющихся Б.-Э. с, наз. системами Бозе, например газом Бозе.

Для идеального квантового газа, т. е. для системы тождественных частиц с массой m без взаимодействия, находящихся в кубе объема V = L³, квантовые одночастичные уровни энергии равны

ε_p = р² /2m,

где р - собственные значения импульса отдельной частицы: р = 2π ħ n/L, n - вектор с целочисленными (положительными, отрицательными или равными нулю) компонентами.

Квантовое состояние идеального газа определяется заданием совокупности чисел заполнения уровней {n_p}, где каждое n_p указывает число частиц в одночастичном состоянии р. Для систем Бозе n_p = 0, 1, 2,....

Для больших систем уровни энергии расположены очень плотно и стремятся к непрерывному спектру при V → ∞. Пусть уровни сгруппированы по малым ячейкам, содержащим G_i уровней в ячейке. Каждой ячейке соответствует средняя энергия ε_i, число предполагается очень большим. Состояние системы определяется набором {N_i}, где N_i есть сумма n_p по уровням ячейки. Статистический вес, т. е. число различных распределений частиц по ячейкам, равен

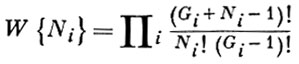
(1)

и определяет вероятность распределения частиц по ячейкам, характеризуемым числами заполнения n₁, n₂ .

Наиболее вероятное распределение, соответствующее заданной энергии Е и числу частиц N:

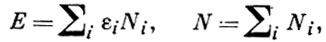
(2)

находится из экстремума (1) при дополнительных условиях (2). Соответствующие средние числа заполнения равны

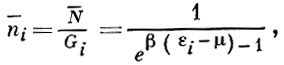
(3)

где р - химич. потенциал β = 1/kТ, k - постоянная Больцмана (универсальная постоянная k = 1, 38 ⋅ 10^{- 16} эрг/град), Т - абсолютная температура. Величины β и μ находятся из условий (2).

Энтропия системы определяется логарифмом статистич. веса (1) для наиболее вероятного распределения (3):

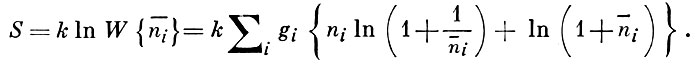
(4)

По энтропии и средней энергии можно найти и другие термодинамич. функции.

Общий подход к Б.-Э. с. состоит в применении большого канонич. Гиббса распределения для вероятности w_n заполнения квантового уровня n всей системы

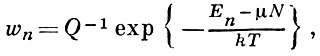
(5)

где

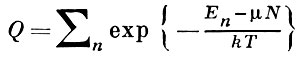
(6)

- статистич. сумма, Е_n - уровни энергии всей системы. Напр., для идеального газа Бозе

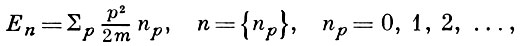
и из (5), (6) может быть получена для чисел заполнения формула (3), а для энтропии - формула (4) без использования комбинаторики. Такой подход особенно важен для неидеальных систем Бозе, когда применение Б.-Э. с. не сводится к простой комбинаторной задаче. В этом случае требования Б.-Э. с. могут быть удовлетворены, если для оператора Гамильтона Н использовать представление вторичного квантования, в к-ром его действие определено в пространстве симметрических волновых функций, или в пространстве чисел заполнения. Тогда статистич. сумма равна

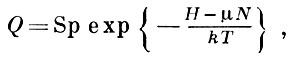
где N - оператор числа частиц, и с ее помощью можно найти все термодинамич. функции системы Бозе.

Лит. : [1] Хуанг К., Статистическая механика, пер. с англ., М., 1966; [2] Кубо Р., Статистическая механика, пер. с англ., М., 1967; [3] Ландау Л. Д., Лифшиц Е. М., Статистическая физика, 2 изд., М., 1964; [4] Шредингер Э., Статистическая термодинамика, пер. с англ., М., 1948; [5] Боголюбов Н. Н., Лекции по квантовой статистике, в кн. : Избр. тр., т. 2, К., 1970.

Д. Н. Зубарев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.