БОГОЛЮБОВА ЦЕПОЧКА УРАВНЕНИЙ

Расстановка ударений: БОГОЛЮ`БОВА ЦЕПО`ЧКА УРАВНЕ`НИЙ

БОГОЛЮБОВА ЦЕПОЧКА УРАВНЕНИЙ (ББГКИ-уравнения - Н. Н. Боголюбов, М. Борн (М. Born), Дж. Грин (G. Green), Дж. Кирквуд (J. G. Kirkwood), Дж. Ивон (J. Yvon) - цепочка уравнений (иерархия) для одночастичных, двухчастичных и т. д. функций распределения классической статистич. системы. Эти функции определяются как

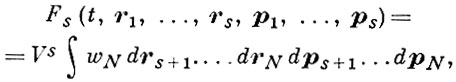
(1)

где s = 1, 2, ..., V - объем системы, a w_N есть N - частичная нормированная на единицу функция распределения, удовлетворяющая Лиувилля уравнению

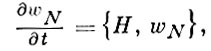
(2)

где фигурные скобки - Пуассона скобки, а Н есть гамильтониан системы. Б. ц. у. в предельном статистич. случае V → ∞, V/N = v = const имеет вид уравнения для F_s со специфич. «зацеплением» с функцией F_{s + 1} более высокого ранга:

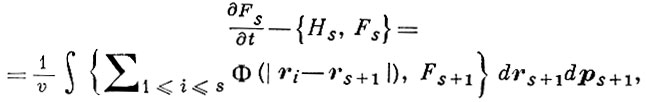
(3)

где Ф(r_i - r_{s + 1}) - потенциал взаимодействия i-й и (s + 1)-й частиц, a H_s - гамильтониан s частиц системы.

В термодинамически равновесном случае, когда распределение по импульсам каждой частицы является Максвелла распределением, рассматриваются s-частичные функции распределения по координатам частиц, к-рые определяются соотношениями типа (1) через N-частичную функцию

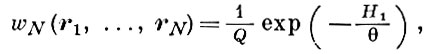
(4)

где H₁ = Н - Н₀, причем Н₀ есть сумма кинетич. энергий частиц системы, а конфигурационный интеграл Q определяется из условия нормировки (4). Б. ц. у. для этих функций имеет вид:

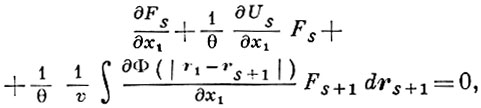
(5)

где U_s - потенциальная энергия взаимодействия s частиц системы.

При помощи функций распределения, гл. обр. F₁ и F₂, могут быть выражены все специфические характеристики статистич. систем. Основные трудности исследования Б. ц. у. (3) или (5) связаны с проблемами замыкания системы (расцепление Б. ц. у.) и решения замкнутой системы со специальными предельными условиями для функций F_s . Это исследование специфично для физич. систем различного типа и наиболее разработано для случаев короткодействия, когда r³₀ /v≪ 1, где r₀ - эффективный радиус взаимодействия частиц друг с другом, и для случаев дальнодействия, когда r³₀ /v≫ 1, в частности для системы с кулоновским взаимодействием. Во временной теории это приводит непосредственно к кинетия. Больцмана уравнению для одночастнчной функции F₁ или к Власова кинетическому уравнению, а в равновесной теории - к вириальному разложению для термодинамич. потенциала или к специфическим кулоновским поправкам.

При рассмотрении квантовых статистич. систем Б. ц. у. составляется для s-частичных статистич. квантовых операторов 〈 x₁, ..., x_s |F_s |x'₁, ..., x'_s 〉, являющихся следами по переменным s + 1, ..., N частиц общего А-частичного оператора - матрицы плотности. Эти уравнения имеют вид, аналогичный уравнениям (3), в к-рых классич. скобки Пуассона заменены квантовыми скобками.

Лит. : [1] Боголюбов Н. Н., Избр. тр., т. 2, К., 1970, с. 99-196; [2] его же, там же, с. 227-493; [3] Уленбек Дж., Форд Дж., Лекции по статистической механике, пер. С англ., М., 1965.

И. А. Квасников.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.