БОГОЛЮБОВА ТЕОРЕМА

Расстановка ударений: БОГОЛЮ`БОВА ТЕОРЕ`МА

БОГОЛЮБОВА ТЕОРЕМА - 1) Б. т. «острие Клина» - обобщение принципа аналитического продолжения, особенно для случая многих комплексных переменных; получена Н. Н. Боголюбовым в 1956 при обосновании дисперсионных соотношений в квантовой теории поля (см. [1], Дополнение А). Современная формулировка: пусть функция f(z), z = (z₁, ..., z_n) = x + iy, голоморфна в открытом множестве T^C_η = [z : |z| < η y ∈ С], где С - такой открытый конус в Rⁿ с вершиной в нуле, что C ∩ (- С) ≠ ∅, открытое множество ⊂ Rⁿ содержится в шаре |х| < η и для любой основной функции φ (х) из () существует

lim ∫ f(х + iy) φ (х) dx, у → 0, у ∈ С,

не зависящий от способа стремления у → 0, у ∈ С; тогда f(z) допускает аналитич. продолжение в область T^C_η ∪ ̃ :

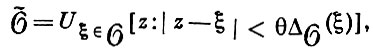
где ̃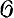 - комплексная окрестность множества 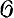, причем 0 < θ < 1 - постоянная, зависящая только от конуса С. а Δ 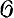(ξ) - расстояние от точки ξ до границы множества 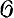. Б. т. «острие клина» остается верной и при η = ∞. В этом случае и при нек-рых предположениях о росте функции f(z) получается первоначальная формулировка Н. Н. Боголюбова (см. [1]; роль конуса играл световой конус в R⁴). Существуют различные доказательства и обобщения этой теоремы (см. [2]). Особо следует отметить обобщения на гиперфункции (см. [4]) и голоморфные коциклы (см. [3]).

Б. т. «острие клина» находит широкие применения в аксиоматич. квантовой теории поля, в теории дифференциальных уравнений с частными производными, в теории граничных значений голоморфных функций (особенно функций многих комплексных переменных). При этом полезным дополнением к теореме является теорема о С - выпуклой оболочке [2]; пусть, в условиях Б. т. «острие клина», С = С⁺ ∪ С^-, С^- = - С⁺, где С⁺ - выпуклый острый конус; тогда

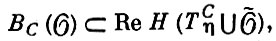
где Н - голоморфности оболочка области 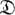, Rе 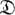- действительное сечение области 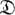, В_C (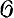) есть С - выпуклая оболочка множества 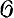, т. е. наименьшее открытое множество, содержащее 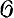и обладающее тем свойством, что если точки х' и х'' из В_C (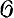) могут быть соединены С - подобной кривой, целиком лежащей в B_C (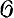), то и все гомотонные ей кривые лежат в B_C ().

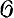Лит. : [1] Боголюбов Н. Н., Медведев Б. В., Поливанов М. К., Вопросы теории дисперсионных соотношений, М., 1958; [2] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [3] Маrtineau A., Distributions et valeurs au bord des fonctions holomorphes - «Théory of Distributions. Proc. of an intern. Summer Institute Held», Lisboa, 1964, p. 193-326; [4] Hyperfunctions and Pseudo-Differential Equations, Lectures Notes in Mathematics, 287, В. - Hdlb. - N. Y., 1973.

В. С. Владимиров.

2) Б. т. об особенностях типа 1/q² : теорема статистич. механики об асимптотич. поведении Грина функций в пределе малых импульсов (q → 0) для бозе- и ферми-систем с градиентно-инвариантным потенциалом взаимодействия. Установлена Н. Н. Боголюбовым в 1961 (см. [1]).

Для систем многих взаимодействующих частиц в случае вырождения состояния статистич. равновесия для двувременных температурных коммутаторных функций Грина в энергетич. представлении справедливо неравенство:

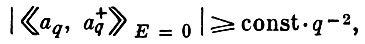
(1)

где a_q, a⁺_q - операторы уничтожения и рождения частицы с импульсом q^→ .

Возникающие (при q → 0), в соответствии с Б. т., у функций Грина особенности отвечают элементарным возбуждениям в исследуемой физич. системе. Б. т. предсказывает также асимптотич. поведение при малых импульсах макроскопич. характеристик системы, связанных с функциями Грина известными формулами.

Согласно (1), напр., для сверхтекучих бозе- (или ферми-) систем плотность непрерывного распределения частиц по импульсам ω (q) при q → 0 стремится к бесконечности не медленнее, чем 1/q² . В этом случае вырождение состояния статистич. равновесия связано с законом сохранения полного числа частиц, т. е. с инвариантностью гамильтониана системы относительно градиентных преобразований. Но аналогичные особенности появляются у соответствующих функций Грина и, следовательно, у корреляционных функций, характеризующих системы с другими видами вырождения, обусловленными наличием нек-рых аддитивных законов сохранения, т. е. инвариантностью гамильтониана системы относительно нек-рых групп преобразований. Б. т. приводит к целому ряду нетривиальных физия, следствий, связанных, напр., с вопросами специфич. упорядочения в системах многих взаимодействующих частиц, спонтанное нарушение симметрии в к-рых проявляется совершенно различным образом: модель Гейзенберга с ферро-, антиферро- и ферримагнитным упорядочиванием, системы сверхтекучего и сверхпроводящего типа, системы с кристаллич. упорядочением.

Возникновение у функций Грина особенностей при q → 0 связывается с наличием в энергетич. спектре системы ветви коллективных возбуждений «бесщелевого» типа, что отвечает при определенном ограничении на потенциал взаимодействия спонтанному нарушению симметрии.

Характер энергетич. спектра элементарных возбуждений может быть исследован с помощью неравенства для построенного на функциях Грина типа (1) массового оператора. Для бозе- систем при конечной температуре (θ ≡ k_B > 0) это неравенство имеет вид:

|Σ₁₁ (0, q ) - Σ₁₂ (0, q )| ≤ const q² . (2)

При q = 0 формула (2) дает обобщение (на конечные температуры) так наз. формулы Гугенгольца-Пайнса. В предположении регулярности массового оператора в окрестности точки (Е = 0, q^→ = 0) из (2) можно получить «бесщелевой» характер (акустич. типа) энергетич. спектра возбужденных состояний.

В случае же нулевых температур (θ = 0) неравенство (1) позволяет установить связь между плотностью непрерывного распределения частиц по импульсам и минимальной энергией возбужденного состояния.

Соотношения типа (1) должны быть справедливы и в квантовой теории поля, где в случае спонтанного нарушения симметрии (при переходе от одного основного состояния к другому) возникает [4], [5] бесконечное число частиц нулевой массы (Голдстоуна теорема), интерпретируемых как особенности при малых импульсах в квантово-полевых функциях Грина. Б. т. перенесена на релятивистскую квантово-полевую модель со спонтанным нарушением симметрии в [6].

Лит. : [1] Боголюбов Н. Н., Избранные труды, т. 3, Киев, 1971; [2] Садовников Б. И., Федянин В. К., «Теор. и матем. физ. », 1973, т. 16, в. 3, с. 368-93; [3] Боголюбов Н. Н. (мл.), Садовников Б. И., Некоторые вопросы статистической механики, М., 1975; [4] Gоldstоnе J., «Nuovo Cim. », 1961, v. 19, p. 154-64; [5] Соldstоne J., Salam A., Weinberg S., «Phis. Rev. », 1962, v. 127, p. 965-70; [6] Казанский А. К., «Теор. и матем. физ. », 1975, т. 22, в. 3, с. 418-21.

А. М. Курбатов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.