БОГОЛЮБОВА НЕРАВЕНСТВО

Расстановка ударений: БОГОЛЮ`БОВА НЕРА`ВЕНСТВО

БОГОЛЮБОВА НЕРАВЕНСТВО в статистической механике, - 1) Б. н. для функционала свободной энергии - неравенство, реализующее вариационный принцип статистич. механики. Для любых эрмитовых операторов U₁ и U₂ справедливо неравенство:

(*)

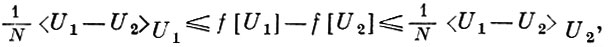
где

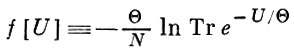
и имеет смысл плотности свободной энергии для системы с гамильтонианом U, аддитивный параметр N - число частиц или объем в зависимости от системы, Θ - абсолютная температура в энергетич. единицах, а

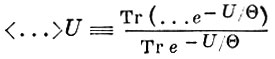
и обозначает термодинамические средние по гамильтониану U.

Б. н. (*) находит применение при получении точных в термодинамич. пределе решений для модельных задач квантовой статистич. физики [1], [2], в исследованиях методом молекулярного поля [3], при доказательстве существования термодинамич. предела, а также для получения физически важных оценок для свободной энергии различных многочастичных систем [4]. Существуют обобщения Б. н. (*) на случай алгебры Неймана со «следом» [5] и общей алгебры Неймана [6].

Лит. : [1] Боголюбов Н. Н., «J. Phisica», 1966, v. 32, p. 933-944; [2] Боголюбов Н. Н. (мл.), Метод исследования модельных гамильтонианов, М., 1974; [3] Тябликов С. В., Методы квантовой теории магнетизма, 2 изд., М., 1975; [4] Кудрин Л. П., Статистическая физика плазмы, М., 1974; [5] Ruskai М. В., «Commun. Math. Phys. », 1972, v. 26, p. 280-289; [6] Araki H., «Соmmun. Math. Phys. », 1973, v. 34, p. 167-178.

2) Б. н. для функций Грина и корреляционных функций. Для двумерных временных температурных коммутаторных функций Грина в энергетич. представлении справедливо неравенство

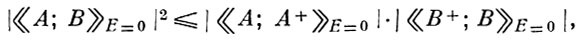
(1)

где ≪...≫ обозначает фурье - образ функции Грина (в энергетич. представлении) от соответствующих операторов в представлении Гейзенберга. Через спектральные представления функции Грина (полагая А = iQ ≡ [Q, H]) Б. н. (1) можно представить в виде:

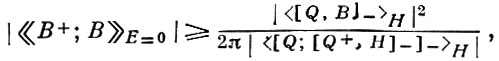
(2)

где 〈...〉_H обозначает термодинамич. средние по гамильтониану системы H, [,] - знак коммутатора; а также можно получить неравенство, мажорирующее (2):

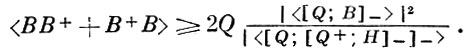
(3)

Общность неравенств (2) и (3) определяет их широкое применение при изучении различных физич. систем.

Улучшение оценок для корреляционной функции

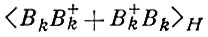
достигается в (3) выбором в качестве оператора Q_k = Q(k) нек-рого «квазиинтеграла» движения, коммутирующего при k = 0 с гамильтонианом системы H. При этом коммутатор в числителе правой части в (3) отражает трансформационные свойства операторов B_k при инфинитезимальных преобразованиях непрерывной группы симметрии, генератором к-рой является оператор Q_{k = 0} . Неравенства (2), (3) эффективно используются при рассмотрении систем со спонтанным нарушением симметрии: термодинамич. средние тогда следует рассматривать в рамках квазисредних метода.

Для функций Грина в классической статистич. механике справедливы аналогичные неравенства, причем соответствующие коммутаторы «переходят» в Пуассона скобки.

Б. н. позволили установить ряд соотношений для модельных систем статистич. физики, исследовать проблему упорядочения в конечных системах и др.

Лит. см. при статье Боголюбова теорема.

А. М. Курбатов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.