БЛЯШКЕ ПРОИЗВЕДЕНИЕ

Расстановка ударений: БЛЯ`ШКЕ ПРОИЗВЕДЕ`НИЕ

БЛЯШКЕ ПРОИЗВЕДЕНИЕ, Бляшке функция, - регулярная аналитич. функция комплексного переменного z, определенная в единичном круге А = {z; |z| < 1} в виде конечного или бесконечного произведения

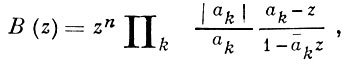
где n - целое неотрицательное число, {a_k}, k = 1, 2, ..., - последовательность точек а_k ∈ K\{0} такая, что произведение в правой части (*) сходится (условие сходимости необходимо лишь в случае бесконечного произведения). Б. п. было введено В. Бляшке [1], установившим следующее утверждение: последовательность {a_k} точек a_k ∈ K\{0} определяет функцию вида (*) тогда и только тогда, когда сходится ряд Σ_k (1 - |a_k |). Каждый множитель вида

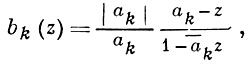
наз. множителем Бляшке для а_k, осуществляет однолистное конформное отображение круга К на себя, переводящее точку z = a_k в нуль, с нормировкой b_k (- a_k /|a_k |) = 1. Множители вида b₀ (z) = z можно интерпретировать как множители Бляшке, соответствующие нулю z = 0 и нормировке b₀ (1) = 1. Определение множителей Бляшке и Б. п. легко переносится на круг произвольного радиуса, а также на любую односвязную область, конформно эквивалентную кругу.

Последовательность 0, ..., 0, а₁, а₂,... (здесь n нулей), обычно выписываемая в порядке неубывания |a_k |, является последовательностью всех нулей Б. п. (*) (каждый нуль выписывается столько раз, какова его кратность). Таким образом, сформулированное выше утверждение Бляшке описывает те последовательности, к-рые являются последовательностями нулей всевозможных Б. п. Произведение (*) можно рассматривать как простейшую ограниченную голоморфную в круге К функцию, имеющую заданную последовательность нулей. Оно сходится абсолютно и равномерно внутри К, представляет в круге К ограниченную голоморфную функцию, |B(z)| < 1, а на ∂К почти всюду имеет угловые граничные значения, по модулю равные 1. Для того чтобы ограниченная голоморфная функция f(z) в К, |f(z)| < 1, была Б. п., необходимо и достаточно, чтобы выполнялось условие

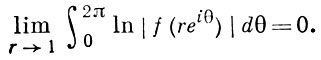
С помощью Б. п. удается дать факторизационное описание важных классов голоморфных функций в единичном круге K. Так, доказана следующая теорема Бляшке: последовательность {а_k} точек круга K является последовательностью всех нулей некоторой ограниченной голоморфной в К функции f(z), |f(z)| < 1, тогда и только тогда, когда ряд Σ_k (1 - |a_k |) сходится. При этом f(z) представима в виде произведения

f(z) = B_f (z)g(z),

где B_f (z) - Б. п., построенное по нулям {a_k} функции f(z), а g(z) - отличная от нуля голоморфная в К функция, |g(z)| < 1, допускающая сравнительно простое интегральное представление. Кроме ограниченных функций, аналогичное факторизационное описание строится для ограниченного вида функций, Харди классов (см. [2]-[4]).

Изложенная теория получила существенное обобщение в работах М. М. Джрбашяна (см. [5], [6]), построившего бесконечные произведения более общей природы, пригодные для факторизации гораздо более широких классов мероморфных функций. Решена также задача построения аналогов Б. п. и теоремы Бляшке для двусвязных [7] и, вообще, конечносвязных [8] областей. Решение проблемы построения удобных аналогов Б. п. для голоморфных функций многих комплексных переменных чрезвычайно затруднено тем обстоятельством, что нули таких функций не могут быть изолированными.

Лит. : [1] Blaschke W., «Веr. Verhandl Sächsisch. Akad. Wiss. Leipzig. Math.-naturwiss. Kl». 1915, Bd 67, S. 194-200; [2] Пpивалов И. И., Граничные свойства аналитических функций, 2 изд., М. - Л., 1950; [3] Неванлинна Р., Однозначные аналитические функции, пер. с нем., М. - Л., 1941; [4] Коллингвуд Э., Ловатер Дж., Теория предельных множеств, пер. с англ., М., 1971; [5] Джрбашян M. М., Интегральные преобразования и представления функций в комплексной области, М., 1966; [6] его же, «Успехи матем. наук», 1973, т. 28, в. 4 (172), с. 3-14; [7] Касьянюк С. А., «Матем. сб. », 1957, т. 42 (84), №3, с. 301-26; [8] Тамразов П. М., «Докл. АН СССР», 1965, т. 161, № 2, с. 308-11.

П. М. Тамразов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.