БЛУЖДАЮЩЕЙ ТРУБКИ МЕТОД

Расстановка ударений: БЛУЖДА`ЮЩЕЙ ТРУ`БКИ МЕ`ТОД

БЛУЖДАЮЩЕЙ ТРУБКИ МЕТОД - один из прямых методов численного решения задач оптимального управления с ограничениями на фазовые координаты и управляющие функции. В Б. т. м. исходная задача оптимального управления в результате дискретизации (по времени Т и фазовому вектору х) и при помощи операции, исключающей управление, сводится к минимизации функции вида

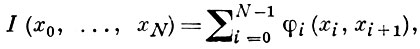
где x_i - значение вектора х в узловых точках гиперплоскостей, заданных в пространстве (t, х) уравнениями t = t_i . Дискретизация по t и х производится с заданными шагами Δ t и Δ x. Каждой совокупности векторов {х₀, x₁, ..., x_N} соответствует ломаная, проходящая через узлы и приближенно представляющая траекторию x(t) исходной задачи оптимального управления. Длина I(x₀, ..., x_N) этой ломаной складывается из длин φ (x_i, x_{i + 1}) отдельных звеньев. Ломаная наименьшей длины находится с помощью рекуррентного соотношения

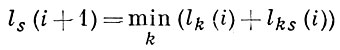
(см. Вариационное исчисление; численные методы).

Поиск глобального минимума на всем полученном графе требует большой оперативной памяти и значительных затрат машинного времени ЭВМ (особенно при дроблении Δ х и Δ t для получения заданной точности решения).

В Б. т. м. ценой отказа от решения задачи отыскания глобального минимума удается резко сократить требуемую память и число операций. В этом алгоритме (имеющем характер последовательных приближений) поиск наилучшей траектории производится не на всем графе, а на подграфе, задаваемом «трубкой», содержащей исходную ломаную - начальное приближение. В каждом сечении трубки содержится заданное количество узлов. Найденная ломаная выбирается за очередное приближение, после чего процесс вычислений повторяется на новом подграфе.

Оценки показывают, что в Б. т. м. число операций растет линейно с увеличением числа узлов сетки по х (с уменьшением шага Δ х), тогда как в методе глобального перебора этот рост квадратичен.

Частным случаем Б. т. м. является локальных вариаций метод, в к-ром число узлов в каждом сечении трубки минимально и равно двум.

Лит. : [1] Моисеев Н. Н., Элементы теории оптимальных систем, М., 1975.

И. Б. Вапнярский, И. А. Ватель.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.