БЛОК-СХЕМА

Расстановка ударений: БЛО`К-СХЕ`МА

БЛОК-СХЕМА - система подмножеств конечного множества, удовлетворяющая нек-рым условиям, связанным с частотой появления пар элементов множества в подмножествах системы. Понятие Б.-с. возникло в теории планирования эксперимента в 20-30-х гг. 20 в., однако под названием тактических конфигураций Б.-с. изучались уже в сер. 19 в. Понятие Б.-с. является вариантом понятий гиперграфа, сети, комплекса. Обычно в Б.-с. на семейства подмножеств накладывается целый ряд дополнительных ограничений. Б.-с. можно задать парой множеств (V, В), где

V = {a₁, ..., a_n}, В = {B₁, ..., B_n}, B_i ⊆ V, i = 1, ..., b.

Элементы множества V наз. элементами Б.-с, а элементы множества В - ее блоками. Элемент а_i и блок B_j инцидентны, если а_i ∈ B_j . Число |B_j | элементов, инцидентных блоку B_j, обозначается обычно через k_j, а число блоков, инцидентных элементу a_i, - через r_i . Через λ_il обозначается число

|{B_j}: a_i ∈ B_j, a_l ∈ B_j |.

Числа v, b, r_i, k_j, λ_il (i, l = 1, ..., v, j = 1, ..., b) наз. параметрами Б.-с. Если r_i = r для всех i = 1, ..., v, k_j = k для всех j = 1, ..., b, а λ_il = λ, то (V, В) есть уравновешенная неполная Б.-с, или BIB-схема (от английского balanced incomplete block design) с параметрами v, b, r, k, λ. Слово «уравновешенный» характеризует одинаковую частоту появлений элементов и пар элементов в блоках, а слово «неполный» служит для указания того, что, вообще говоря, не все k - элементные подмножества входят в В.

Пусть среди чисел λ_il, i, l = 1, ..., v, встречается ровно т различных: λ₁, λ₂, ..., λ_m, и пусть на элементах множества V введено m симметричных отношений связанности так, что выполнены следующие условия:

а) множество V² всех пар элементов множества V разбивается на m непересекающихся подмножеств V²₁, V²₂, ..., V²_m, причем если (a, a') ∈ V²_о, то говорят, что элементы а и а' j-связаны;

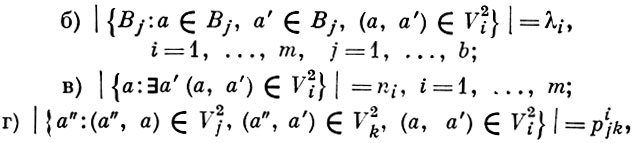
причем в силу симметричности рⁱ_jk = рⁱ_kj, i, j, k = 1, ..., m. Б.-с. со свойствами а)-г) наз. частично уравновешенной Б.-с. c m типами связей, или PBIB(m)-cхемой (от английского partially balanced incomplete block design). Правило, задающее отношение связанности, наз. схемой связанности. BIB-схема является PBIB (1)-схемой. Примером PBIB (2)-схемы является Б.-с, к-рую можно представить в виде таблицы

где любые два числа из одного столбца 1-связаны, а любые два числа, не принадлежащие одному столбцу, - 2-связаны. Здесь v = 12, b = 9, r = 3, k = 4, λ₁ = 1, λ₂ = 0, n₁ = 9, n₂ = 2,

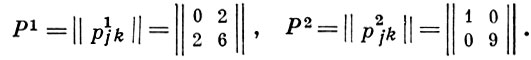
Всякой Б.-с. с v элементами и b блоками соответствует матрица инцидентности А = ||с_ij ||, где с_ij = 1, если a_i ∈ B_j, и с_ij = 0 в противном случае, i = 1, ..., v, j = 1, ..., b. В теории Б.-с. рассматриваются вопросы существования, классификации и вопросы, связанные с построением Б.-с. с заданными параметрами. Параметры Б.-с. связаны определенными соотношениями. Для ВIB-схем справедливы равенства:

vr = kb, (1)

λ (v - 1) = r(k - 1).

Для параметров РВIВ(m)-схем справедливы равенство (1) и следующие соотношения:

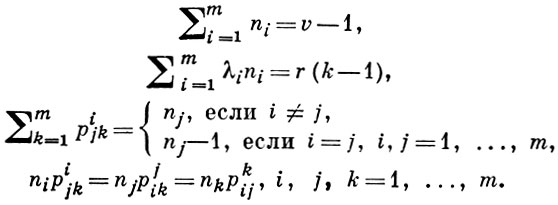
Матрица инцидентности BIB-схемы удовлетворяет основному матричному соотношению

AA^T = (r - λ)E + λ J, (2)

где Е - единичная матрица порядка v, а J - матрица порядка v, составленная сплошь из единиц. Существование (0, 1) - матрицы, удовлетворяющей условию (2), является достаточным условием существования BIB-схемы с заданными параметрами. Из (2) вытекает неравенство b ≥ v. BIB-схема, для к-рой b = v (и значит r = k), наз. симметричной Б.-с, или (v, k, λ)-конфигурацией. Для симметричных ВIB-схем справедлива теорема: если существует симметричная BIB-схема с параметрами v, k, λ, то: а) при v четном k - λ есть квадрат, б) при v нечетном уравнение

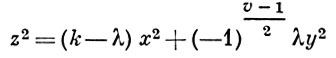
имеет решение в целых числах х, у, z, не равных одновременно нулю. Условия этой теоремы достаточны для существования рациональной матрицы А, удовлетворяющей (2).

Специальный круг вопросов, относящихся к существованию ВIB-схем, возникает в связи с задачей: даны b блоков; каковы условия того, чтобы эти блоки можно было дополнить до BIB-схемы? В наиболее общем виде эти условия выражаются как требования положительной определенности нек-рой квадратичной формы Q, а также возможности представить Q в виде суммы квадратов линейных форм с неотрицательными коэффициентами.

Среди ВIB-схем различают как наиболее изученные следующие подклассы: системы Штейнера (BIB-схемы с λ = 1), в частности системы троек Штейнера (k = 3); адамаровы конфигурации (v = b = 4t - 1, r = k = 2t - 1, λ = t - 1, t ≥ 2), матрица инцидентности к-рых получается из Адамара матрицы; аффинные конечные геометрии и проективные конечные геометрии (см. [1]). В классе PBIB-схем наиболее изучены PBIB (2)-схемы, среди к-рых по виду схемы связанности выделяют так наз. Б.-с. с делимостью на группы, треугольные Б.-с, Б.-с. типа латинского квадрата, циклические Б.-с. и т. д. (см. [3]).

Методы построения Б.-с. принчто разделять на прямые и рекурсивные. Рекурсивные методы позволяют строить с помощью схем с меньшими значениями параметров схемы с большими значениями параметров. В прямых методах обычно используются свойства конечных полей или какие-либо геометрические свойства.

Помимо планирования экспериментов, Б.-с. применяются также в теории игр, теории графов и при построении кодов, исправляющих ошибки.

Лит. : [1] Райзер Г. Дж., Комбинаторная математика, пер с англ., М., 1966; [2] Холл М., Комбинаторика, пер. с англ., М., 1970; 13] Широкова С. А., «Успехи матем. наук», 1968, т. 23, № 5, с. 51-98.

В. Е. Тараканов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.