БИХАРАКТЕРИСТИКА

Расстановка ударений: БИХАРАКТЕРИ`СТИКА

БИХАРАКТЕРИСТИКА, луч, дифференциального оператора - линия, по к-рой происходит касание любых двух характеристик

φ (x₁, ..., x_n) = 0 и ψ (x₁, ..., x_n) = 0

этого дифференциального оператора. Если на Б. ввести параметр s, то ее уравнения x_i = x_i (s), i = 1, ..., n, определяются из решения системы 2n обыкновенных дифференциальных уравнений

(*)

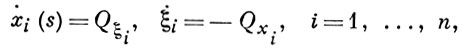
где Q(ξ₁, ..., ξ_n, x₁, ..., x_n) - характеристич. форма дифференциального оператора, точка означает дифференцирование по параметру s, а уравнение Q = 0 при ξ_i = φ_xi - характеристич. уравнение дифференциального оператора. Таким образом, решение x_i = x_i (s); ξ_i = ξ_i (s), i = 1, ..., n, системы (*) задает характеристич. полосу уравнения Q = 0. Эта характеристич. полоса принадлежит характеристике φ (x₁, ..., x_n) = 0, то есть φ (x₁ (s), ..., x_n (s)) ≡ 0, если хотя бы при одном значении s справедливы равенства

φ (x₁ (s), ..., x_n (s)) = 0

и

ξ_i (s) = φ_xi (x₁ (s), ..., x_n (s)), i = 1, ..., n;

тогда эти равенства выполнены при всех значениях s.

Лит. : [1] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964.

Б. Л. Рождественский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.