БИФУРКАЦИЯ

Расстановка ударений: БИФУРКА`ЦИЯ

БИФУРКАЦИЯ - термин, употребляемый в нек-рых разделах математики применительно к ситуации, когда нек-рый объект 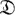= 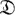(λ) зависит от параметра λ (не обязательно скалярного) и в любой окрестности нек-рого значения λ₀ последнего (бифуркационное значение, или точка Б.) исследуемые качественные свойства объекта 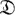(λ) не являются одинаковыми для всех λ. Соответствующие точные определения различны в различных случаях, но в общем они следуют (с теми или иными модификациями) двум вариантам:

а) Изучаемые качественные свойства объекта 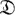состоят в существовании других объектов О, определенным образом связанных с ним. Б. состоит в том, что при изменении λ объекты О возникают или исчезают (в частности, они могут сливаться друг с другом, или из одного объекта может «рождаться» несколько). См. ниже - п. 1).

б) Сначала для объектов 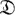(λ) определяется, когда два таких объекта считаются эквивалентными. (Определение должно быть таким, чтобы у эквивалентных объектов все интересующие нас качественные свойства были одинаковыми.) Изменение качественных свойств 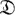(λ) в окрестности точки Б. λ₀, по определению, понимается в том смысле, что там имеются значения λ с неэквивалентными 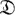(λ). См. ниже - п. 2).

1) В теории операторов исходный объект 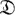(λ) - это нелинейный оператор Ф (х, λ) в действительном банаховом пространстве, с действительным параметром λ, определенный в окрестности точки х = 0 и такой, что ф (0, λ) ≡ 0. Ему при каждом фиксированном λ сопоставляются другие объекты О - решения х нелинейного операторного уравнения Ф (х, λ) = 0. Точка Б. - это точка, в к-рой происходит рождение нового, нетривиального решения этого уравнения. Именно, это такая точка Я0, что для любого ε > 0 существует λ, |λ - λ₀ | < ε, при к-ром уравнение х = Ф (х, λ) имеет решение х(λ), удовлетворяющее условиям 0 < ||x (λ)|| < ε. Если Ф (х, λ) ≡ λ Ах, где A - линейный вполне непрерывный оператор, то понятие точки Б. совпадает с понятием характеристич. значения оператора А.

Если Ф (х, λ) - нелинейный вполне непрерывный оператор, непрерывно дифференцируемый в смысле Фреше и такой, что Ф_x (0, λ) ≡ λ A, то точками Б. оператора Ф могут служить лишь характеристич. значения оператора А. Топологич. методом (см. [1], [2]) установлено, что каждое нечетнократное (в частности, простое) характеристич. значение оператора А является точкой Б. оператора Ф. Аналогичное достаточное условие для случая четнократных характеристических значений формулируется с помощью понятия вращения векторного поля.

Если х = 0 - неизолированное решение уравнения х = Ф (х, λ), то λ₀ есть точка Б. оператора Ф. Вариационным методом доказано (см. [1], [2]), что если Ф (х) - нелинейный вполне непрерывный оператор в гильбертовом пространстве, являющийся градиентом слабо непрерывного функционала, а A = Ф'(0) - вполне непрерывный самосопряженный оператор, то каждое характеристич. значение оператора А является точкой Б. оператора Ф. Понятие точки Б. видоизменяется также на случай больших решений х(λ) → ∞ при λ → λ₀ . Важное значение этих понятий и результатов состоит в том, что при сравнительно слабых ограничениях удается установить ветвление решения х = 0, в частности доказать неединственность решения нелинейной задачи. В ряде случаев более точную информацию дают аналитич. методы теории ветвления решений нелинейных уравнений (см. [5]).

2) В теории гладких динамич. систем рассматриваются однопараметрические (и отчасти двупараметрические [6]) семейства потоков (и каскадов; здесь рассматриваются лишь первые), причем выясняется, когда Б. «типичная», т. е. сохраняет свой характер при малом изменении рассматриваемого семейства [9]; употребительны оба варианта а) и б). При втором два потока считаются эквивалентными, если существует гомеоморфизм фазового пространства, переводящий траектории одного из них в траектории другого с сохранением направления движения. Имеется вполне удовлетворительная теория Б. однопараметрич. семейств потоков с двумерным фазовым многообразием [7], [9], а также локальный вариант, относящийся к окрестности положения равновесия или периодич. решения в n-мерном случае [6].

В варианте а) изучаемые объекты О, к-рые сопоставляются данной динамич. системе, - это положения равновесия и периодич. решения, а иногда также нек-рые инвариантные многообразия (преимущественно торы) и гиперболич. инвариантные множества. Рассматривается «рождение» этих объектов, происходящее как «локально», возле нек-рого положения равновесия или периодич. решения, так и «полулокально», в окрестности «замкнутого контура», образованного несколькими траекториями, к-рые при t → ±∞ стремятся к положению равновесия или к периодич. решениям. Возможен случай Б., к-рая в определенном смысле связана с подобным контуром, но к-рая происходит (с изменением параметра λ) еще до его возникновения [8]. Часто рождение периодич. решений бывает удобно рассматривать, переписывая дифференциальное уравнение и условие периодичности в виде интегрального уравнения и применяя к нему соответствующие методы [5].

3) В теории особенностей отображений встречаются разнообразные Б. различных объектов (как исходных, так и сопоставленных им), в связи с чем имеются различные случаи использования этого термина (вернее, производных от него) (см. [10], [6], [11]), но еще чаще соответствующие понятия получают самостоятельные названия. Таковы, напр., версальные семейства (или деформации) (см. [6], [11], [12]), к-рые (в нек-ром смысле) описывают все возможные Б., могущие произойти при малой деформации рассматриваемого объекта, в частности сюда относятся семь элементарных катастроф [12], к-рые представляют собой «типичные» k - параметрические (k ≤ 4) семейства функций, включающие функцию с вырожденной критической точкой и определенные в окрестности последней; тем самым они описывают соответствующую Б. (Вообще, в иностранной литературе по теории особенностей вместо Б. часто говорят о «катастрофах».)

Лит. : [1] Красносельский М. А., Топологические методы в теории нелинейных интегральных уравнений, М., 1956; [2] Функциональный анализ, М., 1964; [3] Красносельский М. А., Положительные решения операторных уравнений, М., 1962; [4] Вайнберг М. М., Вариационные методы исследования нелинейных операторов, М., 1956; [5] Вайнберг М. М., Треногий В. А., Теория ветвления решений нелинейных уравнений, М., 1969; [6] Арнольд В. И., «Успехи матем. наук», 1972, т. 27, в. 5, 119-84; [7] Андронов А. А., Леонтович Е. А., Гордон И. И., Майер А. Г., Теория бифуркаций динамических систем на плоскости, М., 1967; [8] Гаврилов Н. К., Шильников Л. П., «Матем. сб. », 1972, т. 88, № 4, 475-92; 1973, т. 90, № 1, 139-56; [9] Реiхоtо М. М., в кн. : Proceedings of the International Congress of Mathematics, Vancouver, 19 74, v. 2, p. 315-19; [10] Том P., «Успехи матем. наук», 1972, т. 27, в. 5, 51-7; [11] Арнольд В. И., «Успехи матем. наук», 1975, т. 30, в. 5, 3-65; [12] Вröcker P., Lander L., Differentiable germs and catastrophes, Cambrige, 1975.

Д. В. Аносов, В. А. Треногий.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.