БИРКГОФА ЭРГОДИЧЕСКАЯ ТЕОРЕМА

Расстановка ударений: БИРКГО`ФА ЭРГОДИ`ЧЕСКАЯ ТЕОРЕ`МА

БИРКГОФА ЭРГОДИЧЕСКАЯ ТЕОРЕМА - одна из важнейших теорем эргодической теории. Для эндоморфизма Т пространства X с σ-конечной мерой μ Б. э. т. утверждает, что для любой функции f ∈ L¹ (X, μ) почти всюду (при почти всех х ∈ X) существует предел

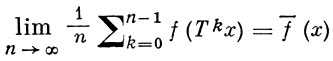
(временное среднее, или среднее вдоль траектории), причем f¯ ∈ L¹ (Х, μ), а если μ (X) < ∞, то

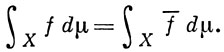
Для измеримого потока {T_t} пространства X с инвариантной σ-конечной мерой μ Б. э. т. утверждает, что для любой функции f ∈ L¹ (X, μ) почти всюду существует предел

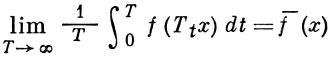
с теми же свойствами f¯.

Б. э. т. была высказана и доказана Дж. Биркгофом [1]. Она подверглась модификациям и обобщениям в различных направлениях (имеются теоремы, к-рые, помимо Б. э. т., охватывают также многие из утверждений несколько иного рода, известные в теории вероятностей как эргодические теоремы; имеются также эргодические теоремы для более общих полугрупп преобразований, см. [2]). Б. э. т. и ее обобщения наз. индивидуальными эргодическими теоремами, т. к. в них речь идет о существовании средних вдоль (почти каждой) отдельной траектории, в отличие от статистических эргодических теорем - эргодической Неймана теоремы и ее обобщений. (В зарубежной литературе сходимость средних почти всюду часто подчеркивают термином point wise ergodic theorem.)

Лит. : [1] Вirkhоff G. D., «Рrос. Nat. Acad. Sci., U. S. A. », 1931, v. 17; [2] Каток А. В., Синай Я. Г., Стёпин А. М., в сб. : Итоги науки и техники. Математический анализ, т. 13, М., 1975.

Д. В. Аносов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.