БИНАРНАЯ ФОРМА

Расстановка ударений: БИНА`РНАЯ ФО`РМА

БИНАРНАЯ ФОРМА - форма от двух переменных, т. е. однородный многочлен

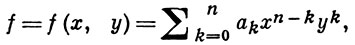
где коэффициенты а_k, k = 0, 1, ..., n, принадлежат заданному коммутативному кольцу с единицей. В качестве такого кольца часто выбирается кольцо ℤ Целых рациональных чисел, кольцо целых элементов нек-рого алгебраического числового поля, поле ℝ действительных чисел или поле ℂ комплексных чисел. Число n наз. степенью формы. Если n = 2, то f наз. бинарной квадратичной формой.

В теории форм можно выделить алгебраическое (теория инвариантов), арифметическое (представление чисел формами) и геометрическое (теория арифметич. минимумов форм) направления. Задачей алгебраич. теории Б. ф. (в ℝ или ℂ) является построение полной системы инвариантов таких форм при линейных преобразованиях переменных с коэффициентами из того же поля (см. Инвариантов теория, а также [2], гл. 5). В арифметической теории Б. ф. изучаются диофантовы уравнения вида

f(x, у) = b,

где а₀, a₁, ..., a_n, b ∈ ℤ - их разрешимость и решения в кольце ℤ. Важнейший результат здесь - теорема Туэ, а также ее обобщения и уточнения (см. Туэ-Зигеля-Рота теорема). О разрешимости таких уравнений в поле ℚ и возможном числе решений см. [5], гл. 9-17, а также Морделла гипотеза. Теория арифметич. минимумов Б. ф. изучается в геометрии чисел. Арифметическим минимумом формы f наз. величина

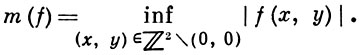
В случае n = 3 доказано, что

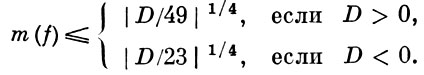
Здесь D - дискриминант формы f, в данном случае равный

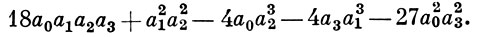
Эти оценки неулучшаемы.

Лит. : [1] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972; [2] Гуревич Г. Б., Основы теории алгебраических инвариантов, М. - Л., 1948; [3] Landau Е., Walfisz A., Diophantische Gleichungen mit endlich vielen Losungen, В., 1959; [4] Lekkerkerker C. G., Geometry of numbers, Groningen [a. o.], 1969; [5] Mоrdell L. J., Diophantine equations, L. - N. Y., 1969.

А. В. Малышев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.