БИНАРНАЯ КВАДРАТИЧНАЯ ФОРМА

Расстановка ударений: БИНА`РНАЯ КВАДРАТИ`ЧНАЯ ФО`РМА

БИНАРНАЯ КВАДРАТИЧНАЯ ФОРМА - квадратичная форма от двух переменных, т. е. форма вида

f = f(x, у) = ах² + bху + су² ; (*)

если а, b, с - целые числа, Б. к. ф. наз. целочисленной. Выражение d = ас - b² /4 наз. определителем, или дискриминантом, Б. к. ф. Иногда под дискриминантом понимается также величина b² - 4ас. Арифметич. теория Б. к. ф. начата П. Ферма (P. Fermat), утверждавшим, что всякое простое число вида 4k + 1 представимо суммой двух квадратов целых чисел. Законченная теория Б. к. ф. построена Ж. Лагранжем (J. Lagrange) и К. Гауссом (С. Gauss). Теория Б. к. ф. - частный случай теории квадратичных форм от n переменных; арифметич. теория Б. к. ф. равносильна теории идеалов квадратичных полей. Теория Б. к. ф. является одним из истоков теории алгебраических чисел.

Число родов Б. к. ф. с определителем d равно 2^{s - 1}, где s - число различных простых делителей числителя d, кроме случаев d ≡ 1 (mod 4), d ≡ 0 (mod 8), когда s увеличивается на 1; при этом, если - d есть квадрат, число родов удваивается. Количество r(d, m) существенно различных примитивных представлений числа m полной системой Б. к. ф. определителя d равно числу решений сравнения

х² ≡ - d(mod m).

Как и в общем случае, имеется алгоритм, сводящий вопрос о решении данного диофантова уравнения 2-й степени с двумя неизвестными (в частности, уравнения f(x, у) = m) к проблеме арифметич. эквивалентности двух Б. к. ф.

Все целочисленные автоморфизмы примитивной формы f с а ≠ 0 представимы в виде

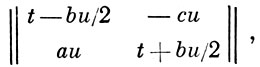
где t² + du² = 1, причем 2t и u - целые числа (см. Пелля уравнение). Поэтому проблема эквивалентности двух форм решается теорией приведения Б. к. ф. Теория приведения положительных Б. к. ф. есть частный случай теории приведения положительных квадратичных форм по Минковскому. Теория приведения целочисленных неопределенных Б. к. ф. сводится к теории приведения квадратичных иррациональностей (см. [2], с. 97-103, [3], с. 170-80).

Важную роль в теории чисел играет арифметич. функция h (d) - число классов целочисленных примитивных Б. к. ф. определителя d. Известно, что h(d) < + ∞. Нек-рое представление о характере роста функции h(d) дает теорема Зигеля: для d > 0 по ε > 0 найдутся постоянные с_ε и с_ε > 0, для к-рых

c'_ε d^{1/2 - ε} < h(d) < c_ε d^{1/2 + ε}

(подобная формула имеет место и для d < 0).

Пусть Δ - целое число, Δ ≡ 1 или 0 (mod 4), причем если s² \Δ, то s = 1 или s = 2, и пусть F = Q(√Δ) есть квадратичное поле, получающееся присоединением √Δ к полю рациональных чисел. Целым идеалам [α₁, α₂ ] поля F ставятся в соответствие целочисленные квадратичные формы

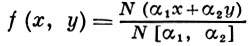
с определителем - Δ /4. Это приводит к взаимно однозначному соответствию (с точностью до перехода к сопряженным классам идеалов) между классами идеалов поля F и классами Б. к. ф. При этом соответствии умножение классов идеалов определяет композицию классов Б. к. ф.

Как и для формы от n переменных, теория Б. к. ф. может быть обобщена на формы вида (*) с коэффициентами а, b, с из заданного алгебраич. числового поля.

Имеются разночтения в определении целочисленной формы, определителя (дискриминанта) формы, эквивалентности форм, класса и рода форм. Приведенное выше определение целочисленной формы принадлежит Л. Кронекеру (L. Kronecker). К. Гаусс требовал (см. [1]), чтобы b было четным. При определении эквивалентности (и класса форм) иногда рассматривают только подстановки определителя + 1; иногда же ±1. В [6] дается более широкое, чем по Гауссу, определение рода.

Лит. : [1] Гаусс К. Ф., Труды по теории чисел, [пер. с нем. и латин.], М., 1959; [2] Венков Б. А., Элементарная теория чисел, М. - Л., 1937; [3] Jones В. W., The arithmetic theory of quadratic forms, N. Y., 1950; [4] Гeльфонд А. О., Линник Ю. В., Элементарные методы в аналитической теории чисел, М., 1962; [5]Landau Е., Vorlesungen tiber Zahlentheorie, Bd 1, Lpz., 1927; [6] Боpeвич 3. И., Шафaревич И. Р., Теория чисел, 2 изд., М., 1972; [7] О'Меаrа О. Т., Introduction to quadratic forms, В., 1963.

А. В. Малышев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.