БИБЕРБАХА МНОГОЧЛЕНЫ

Расстановка ударений: БИБЕРБА`ХА МНОГОЧЛЕ`НЫ

БИБЕРБАХА МНОГОЧЛЕНЫ - экстремальные многочлены, приближающие функцию, к-рая отображает конформно данную односвязную область на круг. Впервые были рассмотрены Л. Бибербахом [1] в связи с задачей о приближенном вычислении конформно отображающей функции.

Пусть односвязная область G расположена в конечной части плоскости и ограничена кривой Г, а функция w = φ (z) отображает эту область конформно и однолистно на круг w < r₀ при условиях φ (z₀) = 0 и φ '(z₀) = 1, где z₀ - произвольная фиксированная точка области G и r₀ зависит от z₀ . Многочлен π_n (z), минимизирующий интеграл

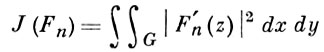
в классе всех многочленов F_n (z) степени n при условиях F_n (z₀) = 0 и F'_n (z₀) = 1, наз. многочленом Бибербаха. В классе всех функций, аналитических в области G и удовлетворяющих тем же условиям, этот интеграл минимизируется отображающей функцией w = φ (z). Если контур Г - жорданова кривая, то последовательность {π_n (z)} сходится к функции φ (z) равномерно внутри области G. В замкнутой области G¯ сходимости может и не быть (см. [2]). Если же контур Г удовлетворяет нек-рым дополнительным условиям гладкости, то последовательность {π_n (z)} сходится равномерно в замкнутой области, причем скорость сходимости зависит от степени гладкости кривой Г.

Лит. : [1] Bieberbach L., Circolo mat. Palermo», v. 38, 1914, p. 98-112; [2] Кeлдыш М. В., «Матем. сб. », 1939, т. 5(47), в. 2, с. 391-401; [3] Мергелян С. Н., Некоторые вопросы конструктивной теории функций, М., 1951; [4] Суетин П. К., «Тр. матем. ин-та АН СССР», 1971, т. 100.

П. К. Суетин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.