
БИБЕРБАХА ГИПОТЕЗА
Расстановка ударений: БИБЕРБА`ХА ГИПО`ТЕЗА
БИБЕРБАХА ГИПОТЕЗА - предположение, высказанное в 1916 Л. Бибербахом [1]: для всех функций f(z) классa S, т. е. для функций f(z), регулярных и однолистных в круге |z| < 1 и имеющих в нем разложение
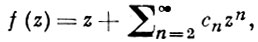
справедлива оценка |cn | ≤ n, n ≥ 2, причем |cn | = n только для функций Кёбе
fθ (z) = z(1 - eiθ z)- 2,
где θ - действительное число. Л. Бибербах доказал справедливость гипотезы только для n = 2. Задача нахождения точной оценки коэффициентов в классе S - частный случай коэффициентов проблемы.
Б. г. простой формулировкой и глубиной привлекла внимание многих математиков и способствовала развитию различных методов геометрич. теории функций комплексного переменного. К настоящему времени (1977) справедливость Б. г. установлена для n ≤ 6. Для n = 3 она была впервые доказана К. Лёвнером (К. Löwner) в 1923 параметрич. методом (см. Параметрических представлений метод); в дальнейшем появились и другие доказательства оценки |с3 | ≤ 3, при к-рых использовались вариационный метод, параметрич. метод, метод экстремальных метрик. Для n = 4 справедливость Б. г. была установлена впервые в 1955 посредством одновременного использования вариационного и параметрич. методов. В 1960 с помощью условии однолистности Грунского оценка |с4 | ≤ 4 была получена значительно проще. Эта оценка была получена также методом вариаций и геометрич. рассуждениями; в другом случае - с использованием неравенств Грунского в матричной форме. Для n = 6 справедливость Б. г. доказана в 1968 с помощью неравенств Грунского, для n = 5 - в 1972 вариационным методом.
Среди других результатов, направленных на доказательства справедливости Б. г., интересны следующие. У. Хейман [4] получил ряд результатов по асимптотич. поведению коэффициентов при n → ∞ функций, р-листных в среднем в |z| < 1, в частности для класса S. Он доказал, что существует предел
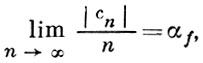
и что αf ≤ 1 со знаком равенства только для функций Кёбе.
Ряд работ посвящен локальной гипотезе Бибербаха, т. е. доказательству того, что функция Кёбе дает max |cn |, по крайней мере для тех функций класса S, к-рые близки к ней в соответствующей топологии (см. Однолистная функция). Установлено, что для каждого n = 3, 4,... существует достаточно малое εn > 0 такое, что для функции f (z) ∈ S, удовлетворяющей условию |с2 - 2| < εn, справедлива оценка Rе сn ≤ n, причем Re сn = n только для f0 (z). Оценка коэффициентов для всех n, точная относительно порядка зависимости от n, была впервые получена в 1925 Дж. Литлвудом (J. Littlewood) сведением оценки коэффициентов к оценке среднеинтегралыюго модуля. Более точные оценки были получены И. Е. Базилевнчем (|cn | < e/2 n + const; 1951), И. М. Милиным (|cn | < 1, 243n, n ≥ 2; 1965).
Лучшая к настоящему времени (1977) оценка получена в 1972 (см. [7]):
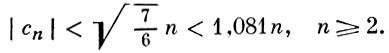
Обзор работ по Б. г. см. в [2], с. 59, 187-90, 571-79, [3], с. 67-121; [9].
Лит. : [1] Bieberbach L., «Sitzungsber. Preub. Akad. Wiss., Phys.-math. Kl. », 1916, S. 940-55; [2] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [3] Милин И. М., Однолистные функции и ортонормированные системы, М., 1971; [4] Науman W. К., «J. London Math. Soc. », 1965, v. 40, № 159, p. 385-406; [5] Оzawa M., «Ködai Math. Semin. Repts», 1969, v. 21, № 1-2, p. 97-132; [6] Pederson R. N.. Schiffer M. M., «Arch. Ration. Mech. and Analysis», 1972, v. 4, 5, № 3, p. 161-93; [7] Fitzgerald С. H., «Arch. Ration. Mech. and Analysis», 1972, v. 46, № 5, p. 356-68; [8] Широков H. A., «Зап. науч. семинаров ЛОМИ АН СССР», 1972, т. 24, с. 182-200; [9] Базилевич И. Е., в кн. : Математика в СССР за 40 лет. 1917-1957, т. 1, М., 1959, с. 444-72.
Е. Г. Голузина.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'