БЕТА-РАСПРЕДЕЛЕНИЕ

Расстановка ударений: БЕ`ТА-РАСПРЕДЕЛЕ`НИЕ

БЕТА-РАСПРЕДЕЛЕНИЕ - непрерывное сосредоточенное на (0, 1) распределение вероятностей с плотностью

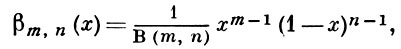
где параметры m, n неотрицательны и нормирующий множитель В(m, n) есть бета-функция Эйлера

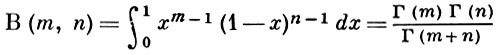
(Г(n) - гамма-функция). Функция распределения выражается через неполную бета-функцию

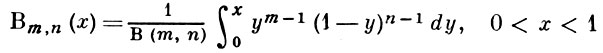
(эта функция табулирована, см. [1], [2]). Моменты Б.-р. выражаются формулой

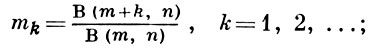
в частности, математич. ожидание и дисперсия равны m/(m + n) и mn/(m + n)² (m + n + 1), соответственно. Если m > 1 и n > 1, то кривая плотности β_{m, n} (x) имеет единственную точку максимума х = (m - 1)/(m + n - 2) и обращается в нуль на концах интервала. Если m < 1 или n < 1, то одна из крайних ординат графика бесконечна, а если и m < 1, и n < 1, то обе ординаты на концах интервала бесконечны и кривая имеет U-образную форму. При m = 1 и n = 1 Б.-р. превращается в равномерное распределение в интервале (0, 1). Другим частным случаем Б.-р. является так наз. арксинуса распределение

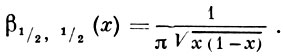
При замене в (1) x = 1/(1 + t) получается распределение с плотностью

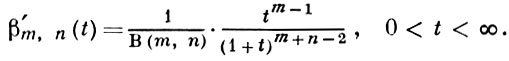
(2)

Это распределение наз. Б.-р. второго рода, в отличие от Б.-р. (1). Распределения (1) и (2) соответствуют распределениям «типа I» и «типа VI» в системе Пирсона кривых. Один из важных случаев возникновения Б.-р. таков: если X₁ и X₂ независимы и имеют гамма-распределения с параметрами m и n соответственно, то случайная величина Х₁ /(Х₁ + Х₂) имеет Б.-р. с плотностью β_{m, n} (x). Этот факт в большой степени объясняет ту роль, к-рую Б.-р. играет в приложениях, в частности в математия. статистике: распределения многих важнейших статистик сводятся к Б.-р. Напр., функция распределения F - отношения

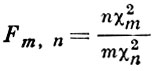
(случайная величина χ²_k имеет χ² - распределение с k степенями свободы) выражается формулой

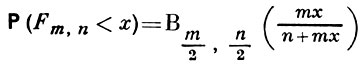
(обычно значения F - распределения вычисляются с помощью таблиц Б.-р.). Функция Б.-р. позволяет также вычислять значения функций биномиального распределения, ввиду соотношения

Б.-р. находит применение не только в математич. статистике, так, напр., плотность Б.-р. является весовой функцией для системы ортогональных Якоби многочленов.

Лит. : [1] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968; [2] Пирсон К., Таблицы неполной бета-функции, пер. с англ., 1974.

А. В. Прохоров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.