БЕССЕЛЯ ФУНКЦИИ

Расстановка ударений: БЕ`ССЕЛЯ ФУ`НКЦИИ

БЕССЕЛЯ ФУНКЦИИ - цилиндрические функции 1-го рода. Б. ф. индекса р может быть определена рядом

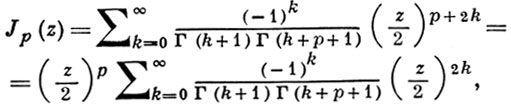
сходящемся на всей плоскости. Б. ф. индекса р является решением соответствующего Бесселя уравнения.

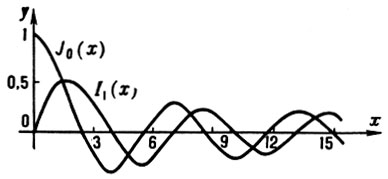
Графики функций y = J₀ (х) и y = J₁ (х).

При действительных положительных значениях аргумента и индекса (p = ν - действительное число) Б. ф. действительна, график ее имеет вид затухающего колебания (см. рис.); при четном индексе Б. ф. четна, при нечетном - нечетна. Поведение Б. ф. в окрестности нуля дается первыми слагаемыми ряда (*); при больших х справедливо асимптотич. представление

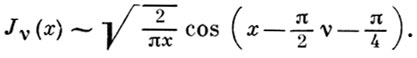
Нули Б. ф. [корни уравнения J_ν (х) = 0] - простые, при этом нули J_ν (х) лежат между нулями J_{ν + 1} (x). Б. ф. «полуцелого» порядка ν = n + 1/2 выражаются через тригонометрич. функции; в частности,

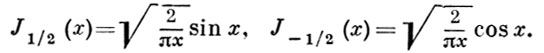
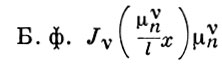
- положительные нули J_ν (x), ν > - 1/2) образуют ортогональную с весом х в промежутке (0, l) систему. При определенных условиях имеет место разложение

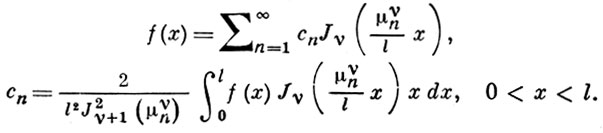
В бесконечном промежутке его заменяет интеграл Фурье-Бесселя

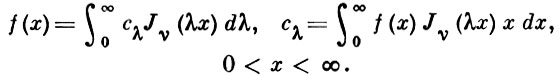
Важную роль в теории Б. ф. и их применений играют:

1) интегральное представление

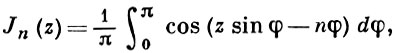
2) производящая функция

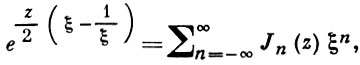
3) теорема сложения для Б. ф. нулевого индекса

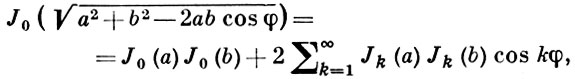
4) рекуррентные формулы

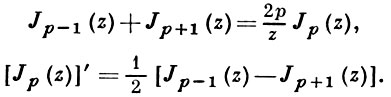
Лит. см. при статье Цилиндрические функции.

П. И. Лизоркин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.