БЕССЕЛЯ УРАВНЕНИЕ

Расстановка ударений: БЕ`ССЕЛЯ УРАВНЕ`НИЕ

БЕССЕЛЯ УРАВНЕНИЕ - линейное обыкновенное дифференциальное уравнение 2-го порядка:

х² у'' + ху' + (х² - ν²)у = 0, ν = const, (1)

или в самосопряженной форме:

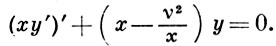
Число ν наз. индексом Б. у. ; величины х, у, ν в общем случае могут принимать комплексные значения. После подстановки y = ux^{- 1/2} получается приведенная форма уравнения (1):

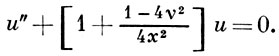
(2)

Б. у. представляет собой частный случай вырожденного гипергеометрического уравнения; уравнение (2) подстановкой x = z/2i приводится к Уиттекера уравнению. Точка х = 0 является для уравнения (1) слабо особой, а точка х = ∞ - сильно особой, и поэтому Б. у. не принадлежит классу Фукса уравнений. Первым систематическое изучение решений уравнения (1) предпринял Ф. Бессель [1], но еще раньше они встречались в работах Д. Бернулли (D. Bernoulli), Л. Эйлера (L. Euler), Ж. Лагранжа (J. Lagrange).

Б. у. возникает при разделении переменных во многих задачах математич. физики (см. [2]), в частности в краевых задачах теории потенциала для цилиндрич. области.

Решения Б. у. наз. цилиндрическими функциями (или бесселевыми функциями). Среди них выделяют цилиндрич. функции 1-го рода (Бесселя функции) J_ν (х), цилиндрич. функции 2-го рода (Вебера функции, или Неймана функции) Y_ν (х), цилиндрич. функции 3-го рода (Ганкеля функции) Н⁽¹⁾_ν (х), Н⁽²⁾_ν (х). Если индекс ν фиксирован, то все эти функции - аналитич. функции комплексного аргумента х; для всех этих функций, за исключением функций J_n (x) целого индекса, точка х = 0 является ветвления точкой. Если же фиксирован аргумент х, то все эти функции являются однозначными целыми функциями комплексного индекса ν (см. [3]).

Если индекс ν не равен целому числу, то общее решение уравнения (1) можно записать в виде

у = C₁ J_ν (х) + C₂ J_{- ν} (х),

где C₁, С₂ - произвольные постоянные. При произвольном индексе любые две из функций J_ν (х), Y_ν (х), Н⁽¹⁾_ν (х), Н⁽²⁾_ν (х) линейно независимы и могут служить фундаментальной системой решений уравнения (1). Поэтому общее решение уравнения (1) представляется, в частности, в следующих формах:

у = C₁ J_ν (х) + C₂ Y_ν (х), у = C₁ Н⁽¹⁾_ν (х) + C₂ Н⁽²⁾_ν (х).

С уравнением (1) тесно связаны: уравнение

z² + zy' - (z² + ν²)у = 0,

переходящее в (1) при подстановке z = ix и имеющее своей фундаментальной системой решений модифицированные цилиндрические функции (бесселевы функции мнимого аргумента), и уравнение

z² y'' + zy' - (iz² + ν²)y = 0,

переходящее в (1) при подстановке z = √i х и имеющее своей фундаментальной системой решений Кельвина функции. Многие другие линейные обыкновенные дифференциальные уравнения 2-го порядка (напр., Эйри уравнение) преобразованием неизвестной функции и независимой переменной также приводятся к уравнению (1); решение ряда линейных уравнений высших порядков удается записать через бесселевы функции (см. [4]).

Подстановка у = х^ν w приводит уравнение (1) к Лапласа уравнению:

xw'' + (2ν + 1)w' + хw = 0;

это позволяет представлять решения уравнения (1) через контурные интегралы на комплексной плоскости.

В приложениях часто возникают задачи на собственные значения для уравнения

x² y'' + xy = + (λ x² - ν²)y = 0 (3)

где ν фиксировано, а λ - параметр. Уравнение (3) на отрезке 0 ≤ х ≤ а с краевыми условиями:

у(х) ограничена при х → 0, у(а) = 0

дает пример задачи с дискретным спектром (собственные значения определяются из условия J_ν (а√λ) = 0 через нули функции Бесселя). Уравнение (3) с краевым условном:

у(х) ограничена на полуоси 0 ≤ х < ∞

представляет собой задачу с непрерывным спектром (собственные значения λ ≥ 0).

Неоднородное уравнение Бесселя

x² y'' + xy' + (x² - ν²)y = f(x) (4)

имеет частное решение

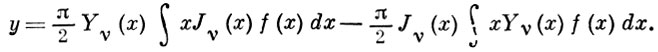
Для правой части специальных видов решения уравнения (4) изучены более детально. Напр., при f(x) = x^ρ уравнению (4) удовлетворяет Ломмеля функция, при

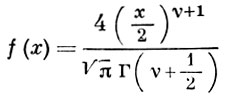
- Струве функция, при

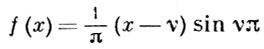
- Ангера функция, при

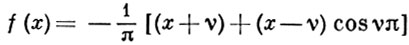
- Вебера функция.

Имеются линейные уравнения высших порядков, свойства решений к-рых аналогичны свойствам бесселевых функций. Общее уравнение типа Бесселя n-го порядка имеет вид

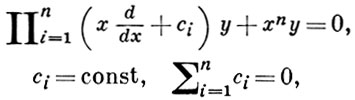
а его решение зависит от n - 1 индексов. В частности, уравнение типа Бесселя 3-го порядка (имеющее решение с двумя индексами α, β) можно представить в форме:

x³ y''' + 3x² y'' + [1 + 9α β - 3(α + β)² ]xy' + [x³ - 9α β (α + β) + 2(α + β)³ ]y = 0, α, β = const.

Лит. : [1] Bessel F., «Abhandl. der Königlichen Akad. Wiss. Berlin», 1824, S. 1-52; [2] Грей Э., Mэтьюз Г., Функции Бесселя и их приложения к физике и механике, пер. с англ., 2 изд., М., 1953; [3] Ватсон Г., Теория бесселевых функций, пер. с англ., ч. 1-2, М., 1949; [4] Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. с нем., 5 изд., М., 1976.

Н. X. Розов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.