БЕССЕЛЯ НЕРАВЕНСТВО

Расстановка ударений: БЕ`ССЕЛЯ НЕРА`ВЕНСТВО

БЕССЕЛЯ НЕРАВЕНСТВО - неравенство

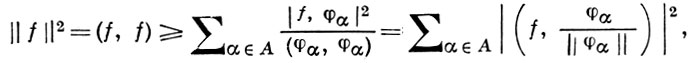
где f - элемент (пред)гильбертова пространства H со скалярным произведением (f, φ), а {φ_α, α ∈ А} - ортогональная система ненулевых элементов из Н. Правая часть Б. н. при любой мощности множества индексов А содержит не более счетного числа слагаемых, отличных от нуля. Б. н. вытекает из тождества Бессе -

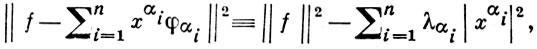
справедливого для любой конечной системы элементов {φ_αi} i = 1, 2,... n. В этой формуле х^α_i - коэффициенты Фурье вектора f по ортогональной системе {φ_α1, φ_α2, ..., φ_αm}, т. е. числа

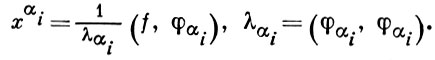
Геометрически Б. н. означает, что ортогональная проекция элемента f на линейную оболочку элементов φ_α, α ∈ A, имеет норму, не превосходящую нормы f (т. е. гипотенуза не короче катета). Для того чтобы вектор f принадлежал замкнутой линейной оболочке векторов φ_α, α ∈ A, необходимо и достаточно, чтобы Б. н. обращалось в равенство. Если это имеет место при любом то говорят, что для системы {φ_α, α ∈ А) в Н выполняется Парсеваля равенство.

Для системы {φ_α, α = 1, 2,...} линейно независимых (не обязательно ортогональных) элементов из Н тождество Бесселя и Б. н. принимают вид

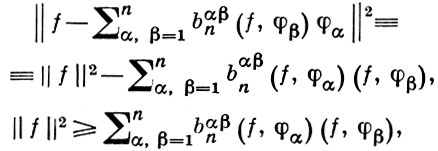
где b^{α β}_n - элементы матрицы, обратной к матрице Грама (см. Грама определитель) первых n векторов исходной системы.

Б. н. предложено Ф. Бесселем (F. Bessel) в 1828 для тригонометрич. системы.

Лит. : [1] Кудрявцев Л. Д., Математический анализ, 2 изд., т. 2, М., 1973.

Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.