БЕССЕЛЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА

Расстановка ударений: БЕ`ССЕЛЯ ИНТЕРПОЛЯЦИО`ННАЯ ФО`РМУЛА

БЕССЕЛЯ ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА - формула, определяемая как полусумма формулы Гаусса (см. Гаусса интерполяционная формула) для интерполирования вперед по узлам

х₀, х₀ + h, х₀ - h, ..., x₀ + nh, x₀ - nh, х₀ + (n + 1)h

в точке x = x₀ + th:

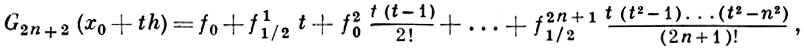
(1)

и формулы Гаусса того же порядка для интерполирования назад по отношению к узлу х₁ = х₀ + h, т. е. по совокупности узлов

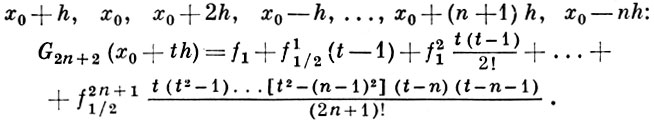
(2)

С использованием обозначения

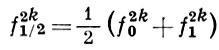
Б. и. ф. имеет следующий вид (см. [1], [2]):

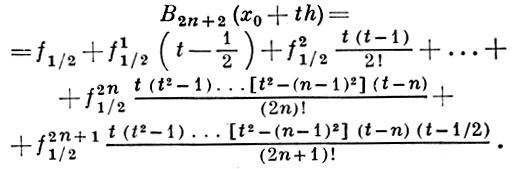
(3)

Б. и. ф. имеет определенные преимущества по сравнению с формулами Гаусса (1), (2); в частности, при интерполировании на середину отрезка, то есть при t = 1/2, все коэффициенты при разностях нечетного порядка обращаются в нуль. Если в правой части (3) отбросить последнее слагаемое, то полученный многочлен B_{2n + 1} (x₀ + th), не являясь собственно интерполяционным многочленом (он совпадает с f(x) лишь в 2n узлах х₀ - (n - 1)h, ..., x₀ + nh), обладает лучшей оценкой остаточного члена (см. Интерполяционная формула), чем интерполяционный многочлен той же степени. Напр., если x = x₀ + th ∈ (х₀, х₁), то оценка остаточного члена для наиболее часто используемого многочлена

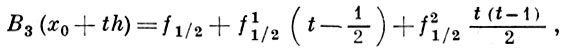
написанного по узлам x₀ - h, х₀, x₀ + h, x₀ + 2h, почти в 8 раз лучше, чем для интерполяционного многочлена, написанного по узлам x₀ - h, х₀, x₀ + h или по узлам х₀, x₀ + h, x₀ + 2h (см. [2]).

Лит. : [1] Березин И. С., Жидков Н. П., Методы вычислений, 3 изд., т. 1, М., 1966; [2] Бахвалов Н. С., Численные методы, М., 1973.

М. К. Самапин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.