БЕССЕЛЕВА СИСТЕМА

Расстановка ударений: БЕ`ССЕЛЕВА СИСТЕ`МА

БЕССЕЛЕВА СИСТЕМА - понятие теории ортогональных систем. Пусть {ψ_n} и {g_n} - две полные системы функций из L² (a, b) = L² (т. е. измеримых функции, интегрируемых с квадратом на отрезке [а, b]), образующие биортогоналъную систему функций. Система ψ_n наз. бесселевой, если для любой функции f ∈ L² сходится ряд

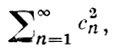
Где с_n (f, g_n) - коэффициенты разложения:

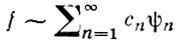
функции f по системе {ψ_n}. Для того чтобы система {ψ_n} была Б. с, необходимо и достаточно, чтобы в пространстве L² можно было определить такой ограниченный линейный оператор А, что система {φ_n}, определенная равенством Aψ_n = φ_n (n = 1, 2,...), является полной ортонормированной системой. Если система ψ_n бесселева, то существует константа М такая, что для любой f ∈ L²

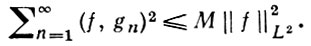
Лит. : [1] Качмаж С., Штейнгауз Г., Теория ортогональных рядов, пер. с нем., М., 1958, с. 430-40.

П. И. Лизоркин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.