БЕССЕЛЕВ ПОТЕНЦИАЛ

Расстановка ударений: БЕ`ССЕЛЕВ ПОТЕНЦИА`Л

БЕССЕЛЕВ ПОТЕНЦИАЛ - потенциал вида

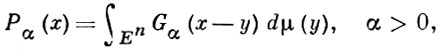
где х = (x₁, ..., x_n), у = (y₁, ..., y_n) - точки евклидова пространства Еⁿ, n ≥ 2, dμ - борелевская мера на Еⁿ,

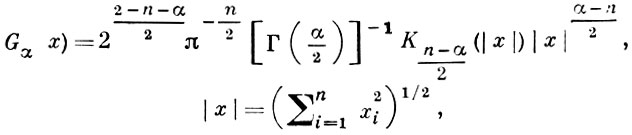
K_ν (z) - модифицированная цилиндрическая функция (или бесселева функция) 2-го рода порядка ν, или функция Макдональда порядка ν'; G_α (х) наз. бесселевым ядром.

Основные свойства бесселевых ядер G_α (х) те же, что ядер Рисса (см. Рисса потенциал): положительность, непрерывность при х ≠ 0, свойство композиции

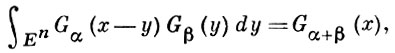
но, в отличие от потенциалов Рисса, Б. п. применимы при всех α > 0, поскольку

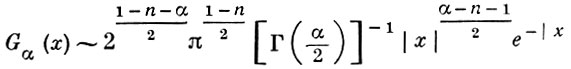
при |х| → ∞.

Если а > 2m, где m - натуральное число, мера dμ абсолютно непрерывна с интегрируемой в квадрате плотностью f(y) ∈ L² (E^2m), то для Б. п. выполняются тождества

(1 - Δ)^m Р_α (х) = Р_{α - 2m} (х),

и

(1 - Δ)^m Р_2m (x) = f(x), где Δ - Лапласа оператор в Е^2m . Иначе говоря, функция G_2m (x) есть фундаментальное решение оператора

Лит. : [1] Никольский С. М., Приближение функций многих переменных и теоремы вложения, М., 1969, гл. 8, [2] Аronszajn N., Smith К. Т., "Аnn. Inst. Fourier", 1961, v. 11 p. 385-475.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.