БЕСКОНЕЧНОСТИ АКСИОМА

Расстановка ударений: БЕСКОНЕ`ЧНОСТИ АКСИО`МА

БЕСКОНЕЧНОСТИ АКСИОМА - аксиома формальной или содержательной теории, обеспечивающая наличие бесконечного количества объектов в рассматриваемой теории. Так, Б. а. в нек-рой системе аксиоматической теории множеств обеспечивает существование бесконечного множества. Напр., в языке аксиоматич. системы Цермело-Френкеля Б. а. обычно записывают в виде:

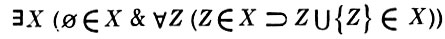
(«существует множество X такое, что ∅ ∈ X и для всякого Z, принадлежащего X, множество Z ∪ {Z} также принадлежит X»).

В простой типов теории, ввиду специфич. ограничений на язык теории, принята другая формулировка Б. а. : существует отношение, к-рое задает на множестве индивидов линейный порядок без последнего элемента. Во многих теориях удобно применять так наз. аксиому бесконечности Дедекинда: существует множество, взаимно однозначно отобразимое в свою собственную часть. С помощью выбора аксиомы нетрудно показать эквивалентность аксиомы бесконечности Дедекинда другим упомянутым формам Б. а. Известно, однако, что без аксиомы выбора эту эквивалентность обычными теоретико-множественными методами доказать нельзя.

В теории множеств употребляются также так наз. высшие аксиомы бесконечности, утверждающие существование множеств весьма высокой мощности: аксиома существования недостижимого кардинала, аксиома существования измеримого кардинала и т. п.

В логике предикатов Б. а. наз. формулы, выполнимые лишь на бесконечном множестве. С точки зрения доказательств теории такие формулы утверждают, вообще говоря, меньше, чем Б. а. в аксиоматич. теории множеств: они обеспечивают бесконечность совокупности объектов исследования, но могут и не обеспечивать существования бесконечного объекта исследования. Показано, что существует бесконечное количество попарно неэквивалентных Б. а. логики предикатов.

А. Г. Драгалин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.