БЕСКОНЕЧНОМЕРНОЕ ПРЕДСТАВЛЕНИЕ

Расстановка ударений: БЕСКОНЕЧНОМЕ`РНОЕ ПРЕДСТАВЛЕ`НИЕ

БЕСКОНЕЧНОМЕРНОЕ ПРЕДСТАВЛЕНИЕ группы Ли - представление группы Ли в бесконечномерном векторном пространстве. Теория представлений групп Ли есть часть общей теории представлений топологич. групп. Специфика групп Ли позволяет использовать в этой теории средства анализа (в частности, инфинитезимальный метод), а также значительно расширить класс «естественных» групповых алгебр (функциональных алгебр относительно свертки), рассмотрение к-рых связывает данную теорию с гармоническим анализом абстрактным, т. е. с частью общей теории топологических алгебр.

Пусть G - группа Ли. Представлением группы G в широком смысле наз. произвольный гомоморфизм G → GL(E), где GL(E) - группа всех обратимых линейных преобразований векторного пространства Е. Если Е - топологич. векторное пространство, то обычно рассматриваются гомоморфизмы со значениями в алгебре С (Е) всех непрерывных линейных преобразований пространства Е, либо в алгебре S (Е) всех слабо непрерывных линейных преобразований пространства Е. Алгебры С(Е), S (Е) наделяются одной из стандартных топологий (напр., слабой или сильной). Представление φ наз. непрерывным (раздельно непрерывным), если вектор - функция φ (g)ξ, непрерывна (раздельно непрерывна) на G × E. Если Е - квазиполное бочечное пространство, то всякое раздельно непрерывное представление непрерывно. Непрерывное представление φ наз. дифференцируемым (аналитическим), если операторная функция φ (g) дифференцируема (аналитична) в S(E). Под размерностью представления φ понимают размерность пространства Е. Важнейшим примером представления группы G является ее регулярное представление φ (g)f(x) = f(xg), х, g ∈ G, определяемое в том или ином классе функций f(x) на группе G. Если G - группа Ли, то ее регулярное представление непрерывно в С (G) и L^p (G) (L^p (G) определяется относительно Хаара меры на G) и дифференцируемо в С^∞ (G) (относительно стандартной топологии в C^∞ (G) - топологии компактной сходимости). Всякое непрерывное конечномерное представление группы G аналитично. Если G - комплексная группа Ли, то естественно рассматривать также ее комплексно аналитические (голоморфные) представления. Как правило, в теории представлений групп Ли рассматриваются только непрерывные представления, и условие непрерывности специально не оговаривается. Если группа G компактна, то все ее неприводимые (непрерывные) представления конечномерны. Соответственно, если G - полупростая комплексная группа Ли, то все ее неприводимые голоморфные представления конечномерны.

Связь с представлениями групповых алгебр. Для группы Ли важнейшими групповыми алгебрами являются алгебра L¹ (G), алгебра C*(G) - пополнение алгебры L¹ (G) по наименьшей регулярной норме (см. Алгебра функций), C₀^∞ (G) - алгебра всех финитных бесконечно дифференцируемых функций на G, М (G) - алгебра всех комплексных мер Радона с компактными носителями на G, D (G) - алгебра всех финитных обобщенных функций (распределений Шварца) на G, а также, для комплексной группы Ли, алгебра A(G) всех аналитич. функционалов над G. Линейные пространства M(G), D(G), A(G) являются сопряженными, соответственно, к C(G), C^∞ (G), H(G), где Н (G) - множество всех голоморфных функций на G (с топологией компактной сходимости). Все эти алгебры наделяются естественными топологиями; в частности, L¹ (G) является банаховой алгеброй - Умножение (свертка) элементов а, b ∈ А, где А - одна из указанных выше групповых алгебр, определяется равенством

ab (g) = ∫ a (gh^{- 1}) b (h) dh

относительно правоинвариантной меры на G, с естественным распространением этой операции на класс обобщенных функций. Интегральная формула

φ (a) = ∫ a (g) φ (g) dg, а ∈ А

устанавливает естественную связь между представлениями группы G и представлениями алгебры А (при условии корректной определенности интеграла): если интеграл слабо сходится и определяет оператор φ (а) ∈ S (Е) при каждом а ∈ А, то отображение а → φ (а) является гомоморфизмом. В этом случае говорят, что представление φ (g) группы G продолжается до представления φ (а) алгебры А, или является А-представлением. Обратно, всякое слабо непрерывное невырожденное представление алгебры А определяется, по указанной формуле, нек-рым представлением группы G (слабо непрерывным при А = М (G), слабо дифференцируемым при A = D (G), слабо аналитическим при А = А (G)). Указанное соответствие сохраняет естественные соотношения между представлениями, такие, как топологич. неприводимость или эквивалентность. Если группа G унимодулярна, то ее унитарным представлениям (в гильбертовых пространствах) соответствуют симметричные представления алгебры L¹ (G) относительно инволюции в L¹ (G) (см. Групповая алгебра). Если Е - секвенциально полное локально выпуклое хаусдорфово пространство, то всякое непрерывное представление группы G в пространстве Е является М (G) - представлением. Если, кроме того, представление группы G дифференцируемо, то оно является D (G) - представлением. В частности, если Е - рефлексивное или квазиполное бочечное пространство, то всякое раздельно непрерывное представление φ (g) является М (G) - представлением, причем φ (а) ∈ С(E) для всех a ∈ M(G).

Инфинитезимальный метод. Если представление φ (g) дифференцируемо, то оно бесконечно дифференцируемо, и пространство Е наделяется структурой 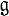- модуля, где 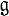- алгебра Ли группы G, путем рассмотрения инфинитезимальных операторов Ли:

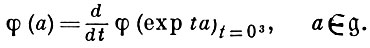
Операторы φ (а) образуют представление алгебры 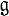, наз. дифференциалом представления φ (g). Вектор ξ ∈ Е наз. дифференцируемым (относительно φ (g)), если вектор-функция φ (g)ξ дифференцируема на G. Вектор ξ ∈ Е наз. аналитическим, если φ (g)ξ - аналитич. функция в окрестности единичной точки e ∈ G. Если φ (g) является C^∞₀ (G) - представлением, то пространство V(Е) всех бесконечно дифференцируемых векторов всюду плотно в Е. В частности, это верно для всех непрерывных представлений в банаховом пространстве; более того, в этом случае [4] пространство W(Е) всех аналитич. векторов всюду плотно в Е. Дифференциал φ (g) в V(Е) может быть приводимым, даже если φ (g) топологически неприводимо в Е. Двум эквивалентным представлениям группы G соответствуют эквивалентные дифференциалы в V(E)(W(E)); обратное, вообще говоря, неверно. Для унитарных представлений в гильбертовых пространствах Е, Н из эквивалентности дифференциалов в W(E), W(H) следует эквивалентность представлений [7]. В конечномерном случае представление группы однозначно восстанавливается по своему дифференциалу. Представление алгебры 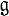наз. интегрируемым (G-интегрируемым), если оно совпадает с дифференциалом нек-рого представления группы G на подпространстве, всюду плотном в пространстве представления. Критерии интегрируемости известны (к 1977) лишь в частных случаях (см., напр., [4]). Если G односвязна, то всякое конечномерное представление алгебры 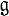является G-интегрируемым.

Неприводимые представления. Одной из основных задач теории представлений является классификация всех неприводимых представлений данной группы G, определяемых с точностью до эквивалентности, при согласованном определении понятий неприводимости и эквивалентности. Так, представляют интерес следующие две задачи. 1) Описание множества Ĝ всех классов унитарной эквивалентности неприводимых унитарных представлений группы G. 2) Описание множества G̃ всех классов эквивалентности по Феллу [7] вполне неприводимых представлений группы G. Для полупростых групп Ли с конечным центром эквивалентность по Феллу равносильна эквивалентности по Наймарку [7], причем имеет место естественное вложение Ĝ → G̃. Множества Ĝ, G̃ естественно топологизируются; при этом топология в них не обязательно хаусдорфова [5]. Если G - компактная группа Ли, то Ĝ = G̃ - дискретное пространство. Описание множества Ĝ в этом случае получено Э. Картаном (Е. Cartan) и Г. Вейлем (Н. Weyl). Линейная оболояка γ (G) матричных элементов группы G (т. е. матричных элементов представлений φ ∈ Ĝ) образует в этом случае подалгебру в C^∞ (G) (алгебру сферич. функций), всюду плотную в C(G) и в C^∞ (G). Матричные элементы образуют базис в C^∞ (G). Если матрицы всех представлений ф ∈ Ĝ определяются в базисе, по отношению к к-рому они унитарны, то соответствующие матричные элементы образуют ортогональный базис в L² (G) (теорема Петера-Beйля). Если группа G некомпактна, то ее неприводимые представления, как правило, бесконечномерны. Метод построения таких представлений, на примере классических матричных групп предложенный И. М. Гельфандом и М. А. Наймарком [1], явился началом интенсивного развития теории унитарных бесконечномерных представлений. Обобщением этого метода для произвольных групп Ли является теория индуцированных представлений Дж. Макки [5]. В 50-х гг. 20 в. начинает развиваться также общая теория неунитарных представлений в локально выпуклых векторных пространствах, основанная в значительной степени на теории топологических векторных пространств и теории обобщенных функций. Детальное описание G̃ (Ĝ) известно (к 1977) для отдельных классов групп Ли (полупростых комплексных, нильпотентных и некоторых разрешимых групп Ли, а также их полупрямых произведений).

Пусть G - полупростая группа Ли с конечным центром, φ есть М (G) - представление в пространстве Е и K-компактная подгруппа в G. Вектор ξ ∈ E наз. K-финитным, если его циклич. оболочка относительно К конечномерна. Подпространство V всех K-финитных векторов всюду плотно в Е и является прямой (алгебраической) суммой подпространств V^λ, λ ∈ K^, где V^λ - максимальное подпространство в V, представление К в к-ром кратно λ. Представление φ наз. K-финитным, если dim V^λ < ∞ для всех λ. Подгруппа К наз. массивной, если всякое вполне неприводимое представление группы G является K-финитным. Принципиальное значение в теории представлений имеет следующий факт: если К-максимальная компактная подгруппа в G, то K массивна. Если векторы из У дифференцируемы, то V инвариантно относительно дифференциала dφ представления φ. Представление φ наз. нормальным, если оно K-финитно и векторы из У слабо аналитичны. Если φ нормально, то существует взаимно однозначное отображение (определяемое сужением на V) замкнутых подмодулей G-модуля φ и подмодулей 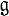-модуля φ₀ = dφ |V, где 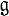- алгебра Ли группы G (см. [7]). Таким образом, изучение нормальных представлений удается алгебраизовать при помощи инфинитезимального метода. Примером нормального представления группы G является ее элементарное представление е(α). Представление е(α) вполне неприводимо для точек α общего положения. В общем случае е(α) допускает разложение в конечный композиционный ряд, факторы к-рого вполне неприводимы. Всякое квазипростое неприводимое представление группы G в банаховом пространстве инфинитезимально эквивалентно одному из факторов е(α), при нек-ром α. Это верно также для вполне неприводимых представлений группы G в квазиполных локально выпуклых пространствах. При этом, если G комплексна, то вместо факторов е(α) достаточно рассматривать подпредставления е(α) (см. [7]). В простейшем случае G = SL(2, ℂ) представление е(α) определяется парой комплексных чисел р, g с целочисленной разностью р - q и действует по формуле правых сдвигов φ (g)f(x) = f(xg), х = (х₁, х₂), g ∈ G в пространстве всех функций f(x) ∈ C^∞ (ℂ² \{0}), удовлетворяющих условию однородности: f(λ x₁, λ x₂) = λ^{p - 1} λ¯^{q - 1} f(x₁, х₂). Если р и g - положительные целые числа, то е(α) содержит неприводимое конечномерное подпредставление d(α) (в классе полиномов от x₁, x₂), фактор по к-рому вполне неприводим. Если р и g - отрицательные целые числа, то е(α) имеет двойственную структуру. Во всех остальных случаях модуль е (α) вполне неприводим. Множество G̃ в этом случае находится во взаимно однозначном соответствии с множеством пар (р, q) (p - q - целое), факторизованном по отношению (р, q) ~ (- р, - q). Подмножество Ĝ состоит из представлений основной серии (р + g - чисто мнимое) (см. Серии представлений), дополнительной серии (0 ≤ р = q < 1) и тривиального (единичного) представления δ₀, к-рое возникает при р = q = 1. Пусть G - полупростая связная комплексная группа Ли, В - ее максимальная разрешимая (борелевская) подгруппа, М - максимальный тор, H = МА - картановская подгруппа, α - характер группы Н (продолженный на В); множество G̃ находится [7] во взаимно однозначном соответствии с A/W, где А - множество всех характеров α, W = W₁ - Вейля группа комплексной алгебры 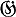. Для характеров «общего положения» представление е(α) вполне неприводимо. Описание множества G сведено к исследованию положительной определенности нек-рых билинейных форм, но окончательное описание (к 1977) неизвестно. Для вещественных групп особый интерес представляет так наз. дискретная серия представлений (прямые слагаемые в L² (G)). Все неприводимые представления дискретной серии классифицированы [3] путем описания характеров этих представлений.

Для нильпотентных связных групп Ли [8] множество Ĝ эквивалентно 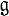'/G, где 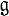' - линейное пространство, дуальное к 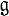, и действие G в 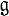' сопряжено присоединенному представлению в 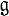[9]. Соответствие устанавливается орбит методом [8]. Подалгебра 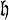⊂ 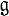наз. поляризацией элемента f ∈ 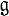', если f аннулирует [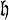, 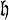] и

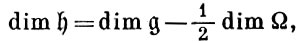
где Ω - орбита f относительно G (всякая орбита четномерна). Если Н - соответствующая аналитич. подгруппа в G и α = ехр f - характер группы Н, то представление u (α), соответствующее f, индуцируется характером α подгруппы Н. При этом u(α₁) эквивалентно u(α₂) тогда и только тогда, когда соответствующие функционалы f₁, f₂ лежат на одной орбите Ω. В простейшем случае группы G = Z(3) всех унипотентных матриц по отношению к фиксированному базису в ℂ³ орбиты общего положения в ℂ³ = {(λ, μ, ν)} являются двумерными плоскостями λ = const ≠ 0 и точками (μ, ν) на плоскости λ = 0. Каждой орбите общего положения соответствует неприводимое представление u(α) группы G, определяемое формулой вида

u (α, g) f (t) = a (t, g) f (t, g), - ∞ < t < ∞,

в гильбертовом пространстве Е = L² (- ∞, ∞). Инфинитезимальные операторы этого представления совпадают с операторами d/dt, iλ t, iλ I, где I - единичный оператор в пространстве Е. Указанный результат равносилен теореме Стоуна-Неймана о самосопряженных операторах Р, Q с коммутационным соотношением [Р, Q] = iλ I. Каждой тояке (μ, ν) соответствует одномерное представление (характер) Z(3). Множество G̃ в этом случае описывается аналогично, с выходом в комплексную область по параметрам λ, μ, ν. Указанный метод орбит естественно обобщается на разрешимые связные группы Ли и даже на произвольные группы Ли, причем в общем случае приходится рассматривать орбиты в 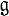'_ℂ, где 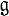'_ℂ - комплексификация 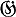', удовлетворяющие нек-рым условиям целояисленности [8].

Исследование общего случая сводится в известной степени к двум рассмотренным случаям посредством теории индуцированных представлений [5], позволяющей описывать неприводимые унитарные представления полупрямого произведения G = HN с нормальным делителем N в терминах неприводимых представлений N и нек-рых подгрупп группы Н (в силу теоремы Леви-Мальцева). Практически этот метод эффективен лишь в том случае, когда радикал коммутативен. Другим методом изучения G̃ (и также G̃) является описание характеров неприводимых унитарных представлений группы G; множество таких характеров находится в естественном взаимно однозначном соответствии с Ĝ. Справедливость общей формулы для характеров, предложенной А. А. Кирилловым [8], проверена (к 1977) лишь для отдельных классов групп Ли.

Гармонический анализ функций нa G. Для компактной группы Ли гармония, анализ сводится к разложению функций f(x), x ∈ G в обобщенные ряды Фурье по матрияным элементам группы G (теорема Петера-Вейля для L² (G) и ее аналоги для других классов функций). Для некомпактных групп Ли основы гармонич. анализа были заложены в [1] введением обобщенного преобразования Фурье

F{α) = ∫ f(x) e (α, х) dx,

где е(α, х) - оператор элементарного представления е (α), dx - мера Хаара на G, и формулой обращения (аналог Планшереля формулы) для L² (G), в случае классических матричных групп над полем G. Этот результат был обобщен на локально компактные унимодулярные группы (абстрактная Планшереля теорема). Преобразование Фурье переводит свертку функций на группе в умножение их (операторных) образов Фурье F (α) и потому является важнейшим инструментом изучения групповых алгебр. Если G - полупростая группа Ли, то операторы F (α) удовлетворяют структурным соотношениям вида

A_s (α) F(α) = F (sα) A_s (α), s ∈ W_i, i = 1, 2, где A_s (α) - сплетающие операторы, W₁ - группа Вейля симметрического пространства G/К (K - максимальная компактная подгруппа в G), W₂ - группа Вейля алгебры 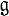_ℂ (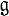_ℂ - комплексификация алгебры Ли группы G). Если функции f (х) финитны, то oпeраторные функции F(α) являются целыми функциями комплексных параметров α. Для групповых алгебр С₀^∞ (G), D(G), где G - полупростая связная комплексная группа Ли, известны аналоги классических Пэли-Винера теорем [7], т. е. дано описание образов этих алгебр относительно преобразования Фурье. Эти результаты позволяют изучить структуру групповой алгебры, ее идеалов и представлений; в частности, они используются при классификации неприводимых представлений группы G. Аналоги теорем Пэли-Винера известны также для нек-рых нильпотентных (метабелевых) групп Ли и для групп движений евклидова пространства.

Проблемы спектрального анализа. Для унитарных представлений групп Ли известна общая процедура разложения представления в прямой интеграл неприводимых представлений [5]. Проблема состоит в отыскании аналитич. методов, осуществляющих это разложение для конкретных классов групп и их представлений, а также в установлении критериев однозначности такого разложения. Для нильпотентных групп Ли известен способ сужения неприводимого представления φ группы G на подгруппу G₀ (см. Орбит метод). Для неунитарных представлений сама постановка задачи требует уточнения, поскольку в классе таких представлений отсутствует свойство полной приводимости. В ряде случаев рассмотрение группы G заменяется рассмотрением одной из ее групповых алгебр A, и задача спектрального анализа трактуется как задача изучения двусторонних идеалов алгебры А. Задача спектрального анализа (и спектрального синтеза) тесно связана также с задачей аппроксимации функций на группе G или однородном пространстве G/H (Н - подгруппа) линейными комбинациями матричных элементов группы G.

Приложения к математической физике. Связь теории представлений групп Ли со специальными функциями математич. физики была отмечена еще Э. Картаном. В дальнейшем было установлено, что основные классы этих функций тесно связаны с представлениями классических матричных групп [10]. Наличие этой связи позволяет с единой точки зрения осветить важнейшие вопросы теории специальных функций: свойства полноты и ортогональности, дифференциальные, рекуррентные соотношения, теоремы сложения и т. д., а также обнаружить новые соотношения и новые классы функций. Все эти функции являются матричными элементами классич. групп или их модификациями (характеры, сферич. функции). Теория разложения по этим функциям - часть общего гармонич. анализа на однородном пространстве G/H. Принципиальная роль теории групп Ли в математич. физике, в частности в квантовой механике и квантовой теории поля, объясняется наличием групповой симметрии (хотя бы аппроксимативной) в основных уравнениях этой теории. Классич. примерами такой симметрии являются принцип относительности Эйнштейна (относительно группы Лоренца), связь таблицы Менделеева с представлениями группы вращений, теория изотопич. спина, унитарная симметрия элементарных частиц и т. д. Связь с теоретич. физикой оказала стимулирующее влияние на развитие общей теории представлений групп Ли.

Лит. : [1] Гельфанд И. М., Наймарк М. А., «Тр. Матем. ин-та АН СССР», 1950, т. 36; [2] Бурбаки Н., Интегрирование. Векторное интегрирование. Мера Хаара. Свёртка и представления, пер. с франц., М., 1970; [3] Воrеl А., Representations de groupes localement compacts, В., 1972; [4] Heлсон Э., Аналитические векторы, «Математика», 1962, т. 6, в. 3, с. 89-131; [5] Макки Г., Бесконечномерные представления групп, там же, с. 57-103; [6] Наймарн М. А., Бесконечномерные представления групп и смежные вопросы, в кн. : Итоги науки. Сер. матем., [в. 2], М., 1964, с. 38-82; [7] Желобенко Д. П., Гармонический анализ функций на полупростых комплексных группах Ли, М., 1974; [8] Кириллов А. А., Элементы теории представлений, М., 1972; [9] Warner G., Harmonic analisis on semisimple Lie groups, v. 1, В., 1972; [10] Виленкин H. Я., Специальные функции и теория представлений групп, М., 1965.

Д. П. Желобенко, М. А. Наймарк.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.