БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ

Расстановка ударений: БЕСКОНЕ`ЧНОЕ ПРОИЗВЕДЕ`НИЕ

БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ - выражение

(*)

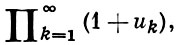
содержащее бесконечное множество числовых или функциональных сомножителей, каждый из к-рых отличен от нуля. Б. п. наз. сходящимся, если существует отличный от нуля предел последовательности частичных произведений

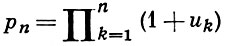
при n → ∞. Значением Б. п. наз. этот предел

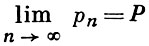
и пишут

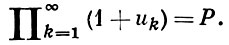
Б. п. сходится тогда и только тогда, если сходится ряд

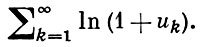
Тем самым исследование сходимости Б. п. сводится к исследованию сходимости рядов. Б. п. (*) наз. абсолютно сходящимся, если сходится Б. п.

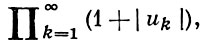
для абсолютной сходимости Б. п. (*) необходимо и достаточно, чтобы абсолютно сходился ряд

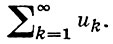
Б. п. обладает переместительным свойством (т. е. его значение не зависит от порядка сомножителей) в том и только в том случае, если оно сходится абсолютно. Б. п. (*) с функциональными сомножителями

1 + u_k = 1 + u_k (z),

определенными, напр., в области D плоскости комплексного переменного z, сходится равномерно в D, если последовательность частичных произведений p_n (z) сходится в D равномерно к пределу, отличному от нуля. В приложениях, однако, весьма важен случай, когда нек-рые сомножители имеют нули в D такие, что на любом компакте K ⊂ D их лежит не более конечного числа. Понятие сходимости обобщается при этом следующим образом: Б. п. (*) наз. (абсолютно, равномерно) сходящимся внутри D, если для любого компакта K ⊂ D существует такой номер N = N(k), что все сомножители 1 + u_k ≠ 0 на k при k ≥ N и последовательность частичных произведений

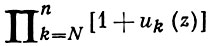
сходится на K (абсолютно, равномерно) к пределу, отличному от нуля. Если все сомножители - аналитич. функции на D и Б. п. сходится равномерно внутри D, то оно представляет в D аналитич. функцию.

Б. п. впервые встретилось у Ф. Виета (F. Viète, 1593) при рассмотрении задачи о квадратуре круга, а именно он получил аналитич. представление числа π, построив следующее Б. п. :

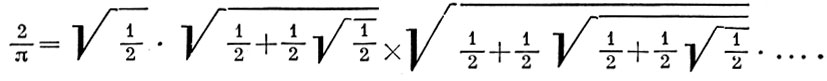
Другое представление числа я восходит к Дж. Валлису (J. Wallis, 1665):

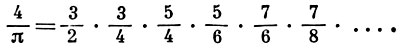
Б. п. с функциональными сомножителями появились у Л. Эйлера (L. Euler, 1742), напр. :

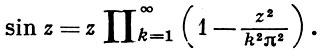
Б. п. - основной аппарат для представления аналитич. функций с явным указанием их нулей; они являются для целых функций аналогом разложения многочлена на множители. См. также Бляшке произведение, Вейерштрасса теорема о бесконечном произведении, Каноническое произведение.

Лит. : [1] Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971; [2] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976; [3] Бицадзе А. В., Основы теории аналитических функций комплексного переменного, 2 изд., М., 1972.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.