БЕСКОНЕЧНОГО ПОРЯДКА УРАВНЕНИЕ

Расстановка ударений: БЕСКОНЕ`ЧНОГО ПОРЯ`ДКА УРАВНЕ`НИЕ

БЕСКОНЕЧНОГО ПОРЯДКА УРАВНЕНИЕ в комплексной области - дифференциальное уравнение вида

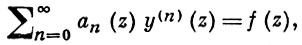
где y(z) - искомая функция комплексного переменного z, a_n (z), f(z) - заданные функции. Наиболее полно изучены Б. п. у. с постоянными коэффициентами:

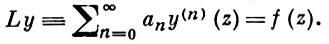
Если характеристич. функция

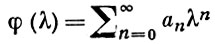
есть целая функция экспоненциального типа σ, то левая часть L_y имеет смысл при z = z₀, когда y(z) - функция, аналитическая в круге |z - z₀ | < R, R > σ. При σ = ∞ необходимо предположить, что y(z) - целая функция. Отличие от уравнения конечного порядка состоит уже в том, что решение y(z) может иметь особенности, даже когда f(z) - целая функция. Если σ = 0 и f(z) есть целая функция, то область существования любого решения выпукла [1]. Общее решение слагается из частного решения и общего решения соответствующего однородного уравнения. Пусть λ₁, λ₂,... - корни характеристич. уравнения φ (λ) = 0 и m₁, m₂,... - соответственно их кратности. Однородное уравнение имеет элементарные частные решения z^k e^{λ_n z} (k = 0, 1, ..., m_n - 1; n = 1, 2,...). Решению однородного уравнения можно отнести по определенному правилу ряд из элементарных решений. Если характеристич. функция φ (λ) имеет правильный рост (в нек-ром определенном смысле), то найдется подпоследовательность частичных сумм этого ряда, сходящаяся к y(z) (см. [4]). В общем случае функцию у(z) можно аппроксимировать с любой точностью конечными линейными комбинациями из элементарных решений [5]. В случае σ = 0 Б. п. у. может иметь неаналитические решения [2]. При нек-рых условиях эти решения образуют квазианалитический класс функций с менее сильными ограничениями на рост производных, чем в классич. теореме Данжуа-Карлемана.

Б. п. у. имеют различные применения: для изучения последовательностей полиномов Дирихле, полноты систем аналитических функций, единственности аналитических и гармонических функций, разрешимости таких проблем анализа, как обобщенная проблема квазианалитичности, обобщенная проблема единственности моментов и т. д.

Лит. : [1] Роlуa G., «Nachr. Ges. Wiss. Göttingen», 1927, S. 187-95; [2] Valirоn G., «Ann. scient. École norm. supér. », 1929, t. 46, № 1, p. 25-53; [3] Лeонтьев А. Ф., «Тр. четвертого всесоюзн. матем. съезда», Л., 1964, т. 2, с. 648-60; [4] его же, «Матем. сб. », 1966, т. 70, № 1, с. 132-44; [5] Красичков-Терновский И. Ф., «Матем. сб. », 1972, т. 88, № 3, с. 331-52.

А. Ф. Леонтьев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.