БЕСКОНЕЧНО УДАЛЕННЫЕ ЭЛЕМЕНТЫ

Расстановка ударений: БЕСКОНЕ`ЧНО УДАЛЕ`ННЫЕ ЭЛЕМЕ`НТЫ

БЕСКОНЕЧНО УДАЛЕННЫЕ ЭЛЕМЕНТЫ, несобственные элементы, - элементы (точки, прямые, плоскости и т. д.), возникающие при расширении нек-рого аффинного пространства до компактного пространства. Б. у. э. являются одной из форм проявления в различных математич. теориях «актуальной» бесконечности. При этом неразрывная связь бесконечного и конечного проявляется в том, что Б. у. э. имеют смысл лишь постольку, поскольку они рассматриваются при нек-рой конкретной компактификации данного «конечного» пространства. Ниже описываются виды Б. у. э., возникающие при наиболее часто применяемых способах компактификации евклидовых конечномерных пространств.

1) Введением Б. у. э. (точек - ∞ и + ∞) числовая прямая ℝ пополняется до компактной расширенной числовой прямой ℝ¯, гомеоморфной отрезку. Другой способ компактификации состоит в погружении ℝ в действительную проективную прямую P₁ (ℝ) = ℝ̃, гомеоморфную окружности S₁ (см. Проективное пространство); при этом R пополняется одной единственной бесконечно удаленной точкой ∞.

2) Добавлением одной единственной бесконечно удаленной точки ∞ конечная комплексная плоскость ℂ пополняется до компактной расширенной комплексной плоскости ℂ¯, гомеоморфной комплексной проективной прямой или Римана сфере S₂ (единичной сфере в евклидовом пространстве ℝ³).

3) Добавлением одной единственной бесконечно удаленной точки ∞ n-мерное действительное числовое пространство ℝⁿ, n ≥ 1, пополняется до компактного расширенного числового пространства R^~n, гомеоморфного сфере S_n ; этот гомеоморфизм наглядно демонстрируется стереографической проекцией. Другой способ компактификации состоит в погружении ℝⁿ в n-мерное действительное проективное пространство P_n (ℝ). При n > 1 эти две компактификации не гомеоморфны.

Например, параллельным прямым в проективной плоскости P₂ (ℝ) соответствует одна и та же бесконечно удаленная точка, непараллельным прямым - различные бесконечно удаленные точки. Все бесконечно удаленные точки плоскости P₂ (ℝ) составляют бесконечно удаленную прямую. Аналогично, в проективном пространстве P₃ (ℝ) каждая плоскость дополнена бесконечно удаленной прямой. Все бесконечно удаленные точки и бесконечно удаленные прямые в P₃ (ℝ) составляют бесконечно удаленную плоскость. Вообще, в P_n (ℝ) все Б. у. э. размерности ≤ (n - 2) составляют бесконечно удаленную (n - 1)-мерную гиперплоскость.

4) Компактификации комплексного n-мерного числового пространства ℂⁿ, n ≥ 1, также возможна посредством погружения ℂⁿ в комплексное n-мерное проективное пространство Р_n (ℂ). В Р_n (ℂ) также все Б. у. э. размерности ≤ (n - 2) составляют комплексную (n - 1)-мерную бесконечно удаленную гиперплоскость. Другой способ компактификации состоит в расширении ℂ до расширенного комплексного пространства ℂ¯ⁿ, представляющего собой топологич. произведение n пространств ℂ¯. При n > 1 пространства Р_n (ℂ) и ℂ¯ⁿ не гомеоморфны. Бесконечно удаленными точками пространства ℂ¯ⁿ являются те наборы z = (z₁, ..., z_n), в к-рых хотя бы одна координата z_ν = ∞. Множество всех бесконечно удаленных точек пространства ℂ¯ⁿ естественно разбивается на n множеств

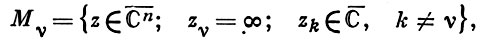
причем каждое M_ν имеет размерность n - 1. Точка (∞, ∞) принадлежит всем M_ν, ν = 1, ..., n. При рассмотрении действительных функций в ℂⁿ применима также одноточечная компактификации ℂ^~n, гомеоморфная ℝ²ⁿ или сфере S_2n .

Лит. : [1] Бурбаки Н., Общая топология. Топологические группы. Числа и связанные с ними группы и пространства пер. с франц., М., 1969; [2] Ефимов Н. В., Высшая геометрия, 5 изд., М., 1971; [3] Хартсхорн Р., Основы проективной геометрии, пер. с англ., М., 1970; [4] Фукс Б. А., Введение в теорию аналитических функций многих комплексных переменных, М., 1962; [5] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.