БЕСКОНЕЧНО МАЛОЕ ИЗГИБАНИЕ

Расстановка ударений: БЕСКОНЕ`ЧНО МА`ЛОЕ ИЗГИБА`НИЕ

БЕСКОНЕЧНО МАЛОЕ ИЗГИБАНИЕ - понятие, первоначально возникшее при описании деформации поверхности F в трехмерном евклидовом пространстве, при к-рой изменение длин кривых на F является величиной порядка малости меньшего, чем изменение пространственного расстояния между точками этих кривых. По существу же в теории Б. м. и. исследуются векторные поля и связанные с ними величины, определенные в точках F и удовлетворяющие тем уравнениям к-рые являются линеаризацией уравнений изгибания F.

Так, если x(u, v, t) - радиус-вектор деформации F_t поверхности F = F₀, то Б. м. и. F характеризуется (начальной) скоростью деформации - вектором

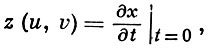
к-рый удовлетворяет уравнению

(dxdz) = 0

или

(x_u z_u) = (x_v z_v) = (x_u z_v) + (x_v z_u) = 0, (1)

где x = x (u, v, 0) - радиус-вектор F. Вектор z, наз. также полем скоростей Б. м. и., или изгибающим полем. Однозначно определяется вектор у такой, что dz = [ydx] - множество точек пространства, описываемое радиус-вектором у, наз. диаграммой вращения Б. м. и. См. также Дарбу поверхности.

В более общей ситуации Б. м. и. многообразия M^k, расположенного в римановом пространстве Vⁿ, представляет собой изометрич. вариацию вложения i: M^k → Vⁿ, т. е. такое векторное поле вдоль вложения

Z ∈ τ (Vⁿ)

где τ (Vⁿ) - касательное расслоение к Vⁿ, к-рое удовлетворяет на M^k уравнению

g(_{∇ X} Z, Y) + g(X, _{∇ Y} Z) = 0; (1')

здесь X, Y ∈ i*τ (M^k) - векторные поля, касательные к вложению, g(⋅, ⋅) - метрическая форма Vⁿ, _{∇ X} - ковариантная произвольная относительно Леви-Чивита связности на Vⁿ, соответствующей g. Поле Z однозначно определяет поле K_Z кососимметрических тензоров типа (1, 1) вдоль вложения: K_Z X = _{∇ X} Z, удовлетворяющее уравнению

_{∇ X} K_Z Y - _{∇ Y} K_Z X + K_Z [X, Y] = R(X, Y)Z,

где R - оператор римановой кривизны Vⁿ .

Если Z индуцируется Киллинга вектором ξ ∈ τ (Vⁿ), т. е. Z = ξ ⋅ i, то соответствующее Б. м. и. (а также и само Z) наз. тривиальным. Если M^k допускает только тривиальные Б. м. и., то оно наз. жестким. См. Жесткость.

При геодезическом отображении F : Vⁿ → Ṽⁿ Б. м. и. M^k ⊂ Vⁿ с вектором Z однозначно соответствует Б. м. и. F(M^k) ⊂ Ṽⁿ с вектором z̃ = F(Z), причем

g̃ (Z̃, F*(Y)) = ψ g (Z, Y),

где ψ - потенциал отображения F. В частности, это соответствие имеет место при проективном преобразовании евклидова пространства (теорема Дарбу-3ауэра) и при геодезич. отображении евклидова пространства в пространство постоянной кривизны (преобразование Погорелова).

Изометрич. вариациям высших порядков соответствуют Б. м. и. высших порядков: для них, в отличие от определенных выше Б. м. и. первого порядка, известны лишь отдельные результаты, в основном касающиеся поверхностей вращения.

Теория Б. м. и. имеет многочисленные приложения в математике и механике, в частности она применяется в задачах изометрич. вложения методом продолжения по параметру, для исследования изометричных поверхностей пространств постоянной кривизны (см. Кон-Фоссена преобразование), в вопросах устойчивости оболочек и т. д.

Лит. : [1] Ефимов Н. В., «Успехи матем. наук», 1948, т 3 в 2(24); [2] Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969; [3] Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957; [4] Векуа И. Н., Обобщенные аналитические функции, М., 1959.

М. И. Войцеховский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.