БЕСКОНЕЧНО МАЛАЯ ФУНКЦИЯ

Расстановка ударений: БЕСКОНЕ`ЧНО МА`ЛАЯ ФУ`НКЦИЯ

БЕСКОНЕЧНО МАЛАЯ ФУНКЦИЯ - функция переменного х, к-рая при данном процессе изменения х становится и остается по абсолютной величине меньше любого заданного числа. Точнее, функция f(x), определенная в окрестности точки х₀, наз. бесконечно малой функцией при х, стремящемся к х₀, если для любого числа ε > 0 найдется такое число δ = δ (ε) > 0, что для всех х, удовлетворяющих условию |х - х₀ | < δ, выполняется |f(x)| < ε. Этот факт записывается так:

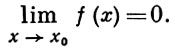
Символ

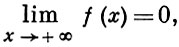
напр., означает, что для любого ε > 0 найдется такое N = N(ε) > 0, что для всех x > N выполняется неравенство |f(x)| < ε. Понятие Б. м. ф. может быть положено в основу общего определения предела функции. Именно, предел функции f(x) при х → х₀ конечен и равен А тогда и только тогда, когда

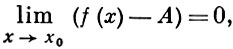
т. е. функция f(x) - А есть Б. м. ф. См. также ст. Бесконечно малых исчисление.

В. И. Битюцков

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.