БЕСКОНЕЧНАЯ ИГРА

Расстановка ударений: БЕСКОНЕ`ЧНАЯ ИГРА`

БЕСКОНЕЧНАЯ ИГРА - бескоалиционная игра, в частности антагонистическая игра, с бесконечными множествами стратегий игроков. Пусть

Г = 〈 X₁, ..., X_n, H₁, ..., H_n 〉

- Б. и. n лиц. К. Берж доказал [см. 1], что если X₁, ..., X_n - локально выпуклые бикомпактные линейные топологические пространства, функции выигрыша H_i непрерывны на Пⁿ_{i = 1} = X_i и квазивогнуты по х_i ∈ X_i, i = 1, ..., n, то в игре Г существуют ситуации равновесия. Показано также [2], что если X_i - бикомпактные хаусдорфовы пространства, H_i непрерывны на Пⁿ_{i = 1} = X_i, i = 1, ..., n, то игра Г имеет ситуации равновесия в смешанных стратегиях. Однако не все Б. и. имеют ситуации равновесия даже в смешанных стратегиях. Напр., для антагонистич. игры, в к-рой пространствами стратегий игроков являются множества целых чисел, а функция выигрыша имеет вид

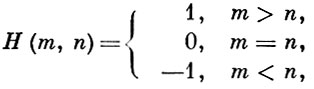
не существует значения. Наиболее исследованным классом Б. и. в нормальной форме являются бесконечные антагонистич. игры и, в частности, игра на единичном квадрате.

Лит. : [1] Берж К., Общая теория игр нескольких лиц, пер. с франц., М., 1961; [2] Гликсберг И. Л., в сб. : Бесконечные антагонистические игры, М., 1963, с. 497-503.

Е. Б. Яновская.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.