БЕСКОАЛИЦИОННАЯ ИГРА

Расстановка ударений: БЕСКОАЛИЦИО`ННАЯ ИГРА`

БЕСКОАЛИЦИОННАЯ ИГРА - система

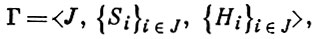
где J - множество игроков, S_i - множество стратегий i-гo игрока, H_i - функция выигрыша i-гo игрока, определенная на декартовом произведении S = П_{i ∈ О} S_i . Б. и. разыгрывается следующим образом: игроки, действуя изолированно (не вступая в коалиции), выбирают свои стратегии s_i ∈ S_i, в результате него складывается ситуация s = П_{i ∈ J} s_i, в к-рой игрок i получает выигрыш H_i (s). Основным принципом оптимальности в Б. и. является принцип осуществимости цели (см. [1]), приводящий к ситуациям равновесия по Нэшу. Ситуация s* наз. ситуацией равновесия, если для всех i ∈ J, s_i ∈ S_i справедливо неравенство

H_i (s*) ≥ H_i (s*||s_i),

где s*||s_i = П_{j ∈ J\i} s*_j × s_i . Таким образом, в одностороннем нарушении договора между игроками, соответствующего ситуации равновесия, не заинтересован ни один из игроков. Было доказано (теорема Нэша), что конечная Б. и. (множества J и S_i конечны) обладает ситуацией равновесия в смешанных стратегиях. Имеются обобщения этой теоремы на бесконечные Б. и. с конечным числом игроков (см. [3]) и на Б. и. с бесконечным числом игроков (см. Неатомическая игра).

Ситуации равновесия s и t наз. взаимозаменяемыми, если любая ситуация r = П_{i ∈} r_i, где r_i = s_i или r_i = t_i, i ∈ J, также равновесна. Они наз. эквивалентными, если H_i (s) = H_i (t) для всех i ∈ J. Пусть Q - множество всех ситуаций равновесия, Q' ∈ Q - множество ситуаций равновесия, оптимальных по Парето (см. Арбитражная схема). Игра наз. разрешимой в смысле Нэша, a Q наз. решением по Нэшу, если все s ∈ Q эквивалентны и взаимозаменяемы. Игра наз. строго разрешимой, если Q' не пусто и все s ∈ Q' эквивалентны и взаимозаменяемы. Антагонистические игры, обладающие оптимальными стратегиями, разрешимы в смысле Нэша и строго разрешимы; однако в общем случае такая разрешимость возможна далеко не всегда.

Имеются другие попытки дополнения принципа осуществимости цели. Так, было предложено (см. [4]) решением Б. и. считать единственную ситуацию равновесия или максиминную ситуацию (выигрыши в последней ситуации каждый из игроков может себе гарантировать независимо от выбора стратегий остальными игроками), выбор к-рой основан на введении нового отношения предпочтения на множестве ситуаций. Иным подходом к определению решения Б. и. является предположение о субъективном прогнозе поведения игроков (см. [5]).

Лит. : [1] Воробьев Н. Н., «Успехи матем. наук», 1970, т. 25, № 2 (152), с. 81-140; [2] Нэш Дж., в сб. : Матричные игры, М., 1961, с. 205-21; [3] Гликсберг И. Л., в сб. : Бесконечные антагонистические игры, М., 1963, с. 497-503; [4] Harsanyi J. С., в кн. : Advances in game theory, Princeton (N. Y.), 1964, p. 651-79; [5] Вилкас Э. Й., «Теория вероят. и ее примен. », 1968, т. 13, в. 3, с. 555-60.

Э. Й. Вилкас, Е. Б. Яновская.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.