БЕРНШТЕЙНА-РОГОЗИНСКОГО МЕТОД СУММИРОВАНИЯ

Расстановка ударений: БЕРНШТЕ`ЙНА-РОГОЗИ`НСКОГО МЕ`ТОД СУММИ`РОВАНИЯ

БЕРНШТЕЙНА-РОГОЗИНСКОГО МЕТОД СУММИРОВАНИЯ - один из методов суммирования рядов Фурье; обозначается (БР, α_n). Тригонометрич. ряд

(*)

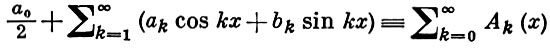
суммируется методом Бернштейна-Рогозинского в точке х₀ к значению S, если выполняется условие

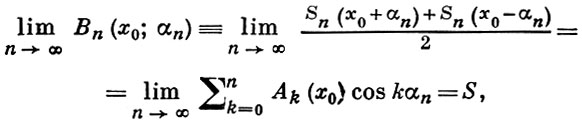
где {α_n}, α_n > 0, α_n → 0, - числовая последовательность, a S_n (x) - частичные суммы ряда (*).

В. Рогозинский (см. [1]) сначала рассмотрел (1924) случай α_n = рπ /2n (р - нечетное число), потом (1925) общий случай. С. Н. Бернштейн (см. [2]) рассматривал (1939) случай α_n = π /(2n + 1). (БР, α_n) - метод суммирует ряд Фурье функции f(x) ∈ L[0, 2π] в случаях α_n = рπ /2n и α_n = π /(2n + 1) в точках непрерывности функции к ее значению и является регулярным методом суммирования.

Суммы В_n (х, α_n) Бернштейна-Рогозинского применяются как аппарат приближения. В обоих указанных выше случаях они осуществляют приближение того же порядка, что и наилучшее приближение для функций из классов Lip α и W¹ Lip α.

Лит. : [1] Rogosinski W., «Маth. Ann. », 1925, Bd 95, № 1, S. 110-34; [2] Бернштейн С. H., Собр. соч., т. 1, М., 1952, с. 523-25; [3] Стечкин С. Б., Методы суммирования С. Н. Бернштейна и В. Рогозинского, в кн. : Г. Харди, Расходящиеся ряды, пер. с англ., М., 1951.

А. А. Захаров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.