БЕРНШТЕЙНА МНОГОЧЛЕНЫ

Расстановка ударений: БЕРНШТЕ`ЙНА МНОГОЧЛЕ`НЫ

БЕРНШТЕЙНА МНОГОЧЛЕНЫ - алгебраические многочлены, определяемые формулой

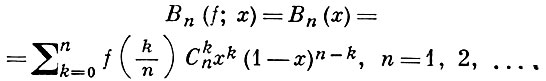
Введены С. Н. Бернштейном в 1912 (см. [1], т. 1, с. 13). Последовательность Б. м. сходится к функции f(x) равномерно на отрезке 0 ≤ x ≤ 1, если функция f(x) на этом отрезке непрерывна. Для функции, ограниченной в точке С. 0 < С < 1, имеющей разрыв 1-го рода, имеем

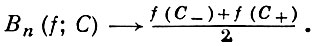
Справедливо равенство:

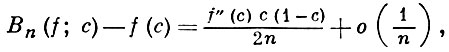
если в точке с функция f(x) дважды дифференцируема. Для функции, k-я производная f^(k) (x) к-рой непрерывна на отрезке 0 ≤ х ≤ 1,

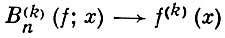
равномерно на этом отрезке. Исследовалась сходимость Б. м. в комплексной плоскости, если f(x) - аналитическая на отрезке 0 ≤ х ≤ 1 функция (см. [1], т. 2, с. 310, и [5]).

Лит. : [1] Бернштейн С. Н., Собр. соч., т. 1, М., 1952, с. 105-06; т. 2, М., 1954, с. 310-48; [2] Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954, гл. 2; [3] Баскаков В. А., «Докл. АН СССР», 1957, т. 113, № 2, с. 249-51; [4] Коровкин П. П., Линейные операторы и теория приближений, М., 1959, с. 117-24; [5] Канторович Л. В., «Изв. АН СССР. Сер. матем. », 1931, № 8, с. 1103-15.

П. П. Коровкин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.